Nesse artigo, vamos ver uma introdução às equações diferenciais parciais. De fato, as equações diferenciais constituem uma importante parte do arcabouço matemático das ciências aplicadas ao passo que permitem a modelagem de diversos fenômenos. Por outro lado, essas equações também formam uma grande área de pesquisa dentro da análise matemática, em particular, as equações diferenciais parciais EDPs tomam um grande destaque nesse cenário.
Tendo isso em vista, nesse artigo vamos falar sobre as EDPs e claro, vamos falar das principais EDPs que podem aparecer na sua prova de cálculo avançado. Vem comigo gurunauta que hoje, vamos matar esse assunto.
O que são Equações diferenciais parciais
A ideia que rege as EDPs é similar ao que vimos nas EDOs. Na verdade, a própria noção e ideia dessas equações é praticamente a mesma, todavia, há uma diferença importante: o tipo de derivada envolvida.
De fato, aqui consideraremos funções com mais de uma variável. Consequentemente, vamos adentrar no cálculo de funções de várias variáveis, logo, as derivadas aqui não serão totais e sim parciais. Em virtude disso, é que definimos a noção de EDP. Essencialmente, é uma equação onde a função incógnita encontra-se associada as derivadas parciais da função.
Nesse sentido é interessante relembrarmos as notações que expressam a derivada parcial de uma função. Com efeito, vamos considerar uma função u que dependa das variáveis x e t, logo teremos o seguinte
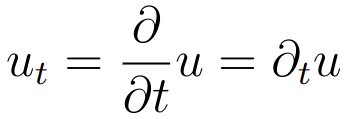
No caso das derivadas segundas teremos as seguintes notações
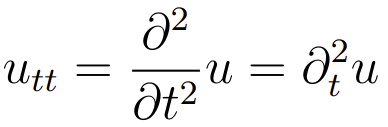
Ademais, veja que fora essa diferença as análises sobre homogeneidade, linearidade, ordem e grau feitas no artigo valem de forma exatamente igual para as EDPs.
Métodos de solução para EDPs? existe ?
Um dos problemas fundamentais que vimos na teoria das equações diferenciais é a determinação de soluções para uma dada equação. De fato, no contexto das EDOs vimos que para as equações lineares de primeira ordem há uma forma explícita para solução, além de que para um certo tipo de equações de segunda ordem é possível determinarmos também uma forma fechada para resolvermos essas equações.
Todavia, quando estamos no contexto das EDPs temos um problema ainda maior. Aqui, por vezes, não teremos uma forma explícita para resolvermos a equação e isso vale independentemente da ordem.
Entretanto, há métodos gerais que podem ser empregados para tal objetivo. Evidentemente, cada método necessitaria bem mais do que 500 palavras para ser comentado, assim, vamos apenas citá-los por hora
- Transformada de Fourier,
- Transformada de Laplace,
- Separação de Variáveis,
- Métodos numéricos (Ruggen-Kuta, Newton, … ),
- Quadratura.
Conheça algumas equações diferenciais parciais
Como já falado algumas equações diferenciais parciais são associadas a fenômenos físicos importantes. Tendo isso em mente, veja algumas das EDPs mais conhecidas e importantes

Bem gurunauta, espero que tenha curtido o artigo. Agora, fica ligado na MeuGuru e no nosso blog que vamos sempre ter novidades para você.





