O cálculo de limites de funções é uma ferramenta importante para o estudo de funções. Além disso, é um dos pontos altos da cadeira de cálculo 1 nos cursos de exatas e engenharias. Pensando nisso, nesse artigo trazemos as principais tópicos para que você entenda o que é o limite de uma função e como fazer para calcular esses limites.
O que é o limite de funções ?
Primeiro, vamos começar a entender o que é o limite de uma função. De fato, os limites podem ser entendidos como uma ferramenta para avaliarmos o comportamento de funções quando elas se aproximam de um certo valor.
Para explicar isso melhor, vamos escolher uma função f:R -> R e um ponto “a”, onde o ponto “a” não necessariamente faz parte do domínio da função. Agora, como “a” pode ou não estar no domínio da função nós, não podemos simplesmente calcular f(a), pois isso sequer fará sentido. Todavia, uma forma de contornar calcular f(x) para quando x está muito próximo de “a”, ou seja, x tende ao valor “a” tanto quanto se queira. Esse cálculo, é na verdade, o limite de f(x) quando x tende a “a” e esse procedimento é escrito da seguinte forma:

onde L, é o valor do limite. Além disso, essa escrita é apoiada numa definição matemática rigorosa e precisa

Só que não precisamos dela para nossos objetivos. Entretanto, podemos visualizar essa definição com auxílio da Figura 1.
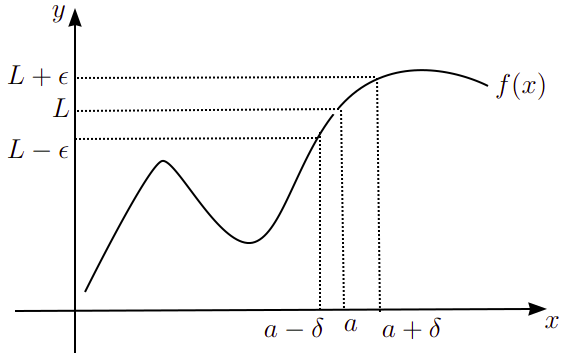
Na verdade, o que a definição e a Figura 1 querem dizer é o seguinte. Se perto do valor “a”, pegarmos um intervalo suficientemente pequeno (a-delta,a+delta) que contém o valor a, então, o valor de f(x) ficará cada vez mais próximo do intervalo (L-epsilon,L+epsilon), logo, f(x) = L para quando x tender ao valor “a”.
Resumidamente, f(x) se aproxima de L a medida que x se aproxima de a. Ademais, é importante dizer que há vários tipos de limites, onde inclusive os valores “a” e “L” podem ser mais ou menos infinitos, mas isso é papo para outro artigo. Aqui, vamos trabalhar apenas com limites finitos!.
Fatorações para o cálculo de limites
Agora, vamos ao cálculo do limite de funções. Para isso, vamos mostrar dois exemplos do tipo mais frequente de limites finitos que aparecem nas provas e listas de cálculo:
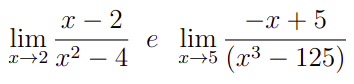
A tarefa aqui seria resolver esses dois limites. Mas veja, apenas entender o que é não te ensina a como resolver não é mesmo?. Bom, de fato, agora você vai precisar de um pouco de técnica. Mas relaxa, continua comigo que você vai sair daqui sabendo responder esses dois exercícios.
Como já foi dito, o cálculo de limites é feito aproximando x suficientemente do valor desejado. Na prática, vamos acabar realmente substituindo o valor de x por esse número. Bom, então, vamos fazer isso para os limites acima
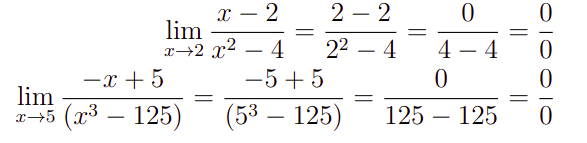
Entretanto, esses limites pertencem a uma classe de problemas que possui uma forma de remover os termos que fazem essas indeterminações acontecerem. Para isso, vamos presentar duas fórmulas de fatoração, a diferença de quadrados e diferença de cubos, para você guardar no peito e arrasar na sua prova, essas são respectivamente:
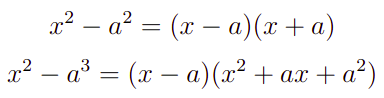
Agora, basta notar que x²-4=x²-2² e que x³-125=x³-5³. Ou seja, os denominadores do nosso exemplo podem ser fatorados com as fórmulas anteriores.
Caso você queira ver outros exemplos de fatoração, recomendo que você veja o artigo sobre como fatorar polinômios.
Cálculo de limites de funções passo a passo
Agora que conhecemos as fatorações, podemos calcular esses exemplos. Para o primeiro limite temos o passo a passo:

Para o segundo limite, o desenvolvimento é um pouquinho maior, mas segue a mesma ideia, veja
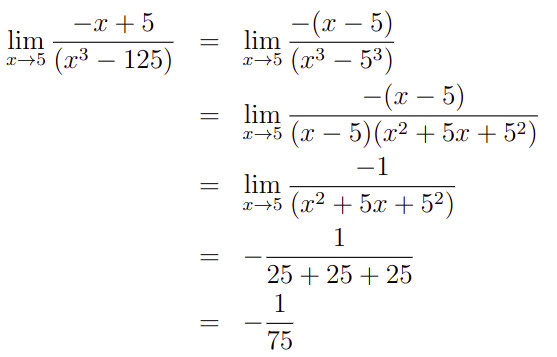
E com isso, aprendemos a resolver os limites com o uso de fatoração para a diferença dos quadrados e diferença dos cubos.
Agora é a sua vez, coloque a mão na massa e arrase nos estudos e garanta sua aprovação no semestre. E lembre-se, conte sempre com a MeuGuru para te auxiliar em tudo que você precisar!.





