Nesse artigo, vamos mostrar como calcular a área de uma curva y=f(x) qualquer com exemplos.
Eae gurunauta, esse artigo foi escrito pensando em te salvar daquelas questões de cálculo de áreas sob curvas com integrais. Isso mesmo, nesse texto vou te ensinar a como calcular a área de regiões do plano com uso de integrais de funções de uma variável. Então, já confere o texto e garanta a sua aprovação no semestre.
Como calcular a área de uma curva ?: Aplicações das integrais.
No cálculo 1, somos apresentados a três importantes conceitos: limites, derivadas e integrais. Esses conceitos formam a base do cálculo e são como novas ferramentas para começarmos os estudos no ensino superior. Além disso, esses conceitos trazem a nós aplicações fantásticas, em particular, as integrais.
Em particular, essas foram desenvolvidas por Leibniz e Newton tendo como motivação a tentativa de determinar a área abaixo de uma função. Visto que, determinar a área de certas funções traria informações sobre o movimento dos corpos além de generalizar resultados da geometria plana.
Então, agora que você já entendeu a importância desse assunto, vamos ao que interessa: como calcular a área de uma curva. Matematicamente, dada uma função y=f(x) contínua a área, A, da curva abaixo de f(x) no intervalo [a,b] é dada por:
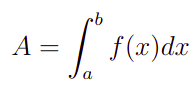
Portanto, determinar a área abaixo de um gráfico y=f(x) é exatamente calcular a integral definida nos extremos do intervalo em que a função é definida.
Todavia, vamos destacar algumas observações. Primeiramente, a função f(x) deve ser contínua, caso contrário o valor de A não será preciso.
Além disso, é possível calcular, também, a área entre duas curvas, por exemplo f(x) e g(x). Nesse caso, a fórmula da área A é a seguinte.

Em que, consideramos os mesmos intervalos de integração (os pontos a e b).
Com isso, sim, apenas sabendo isso você pode calcular as áreas para quaisquer curvas. Por isso, vou te mostrar, agora, como você vai fazer isso. Então, vamos para os exemplos.
Exemplos importantes: Como calcular a área da função f(x)
Hora de por a mão na massa e para isso, começaremos com um problema bem simples. Vamos calcular a área da região abaixo da curva y=f(x) =x com x entre 0 e 2. Essa região é mostrada na Figura 1.
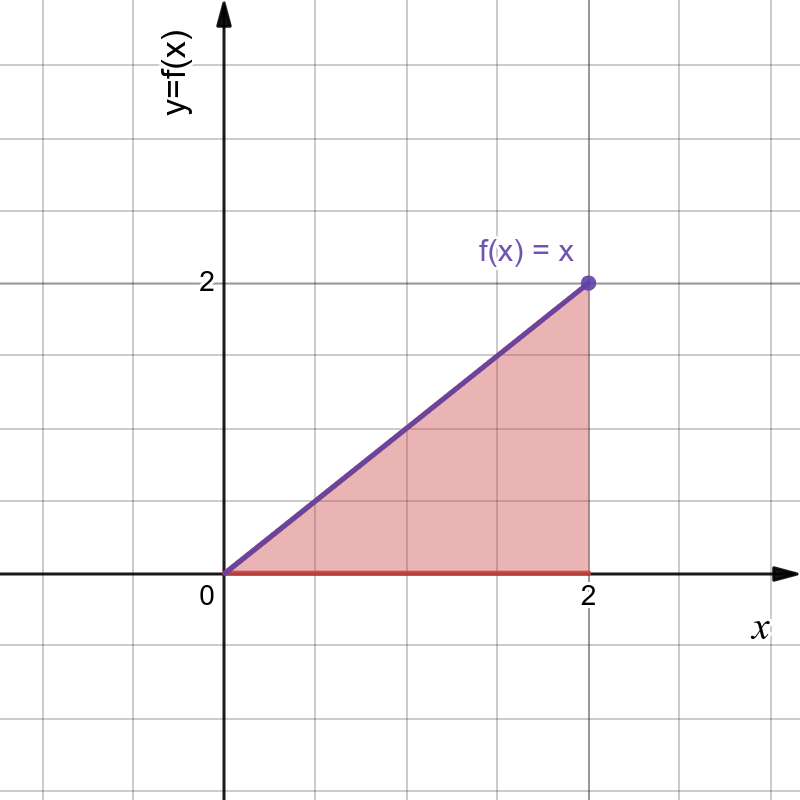
Portanto, para nós calcularmos a área A, basta usarmos a primeira fórmula que eu te apresentei. Com efeito, teremos:
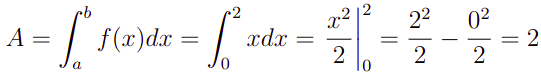
ou seja, a área é A =2 u.a (unidades de área). Por outro lado, a figura geométrica formada por essa curva é um triângulo retângulo de base b=2 e altura h=2 basta você ver a Figura 1. Tendo isso em vista, vamos calcular a área usando a fórmula da geometria plana, com efeito nós teremos

Oras, obtemos o mesmo resultado. De fato, isso ocorre por que com a integral, podemos generalizar todas as fórmulas de áreas de figuras planas que existem. Esse é um exemplo que ilustra esse fato.
Vamos ao segundo dos nossos exemplos.
Exemplos importantes: Cálculo da área entre curvas
Vamos ao segundo dos nossos exemplos. Aqui vamos calcular a área entre duas curvas f(x) = x² e g(x) = x entre 0 e 1. Bom, o que queremos é determinar a região de azul entre esses gráficos que aparece na Figura 2.
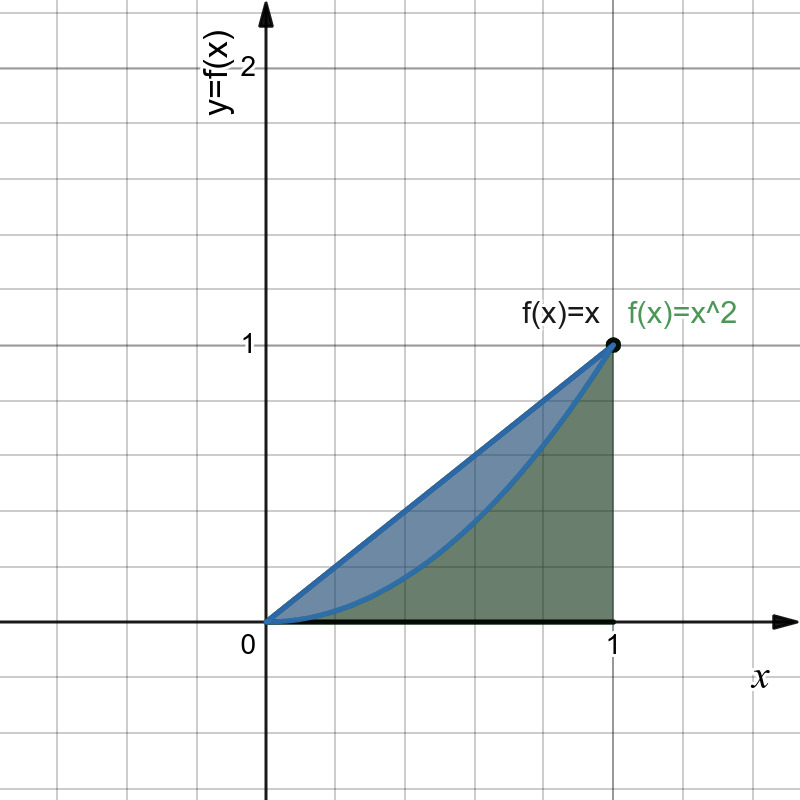
Com isso, vamos usar a segunda fórmula para A. Bom você deve ter visto que nela tem um módulo, porém você não precisa se preocupar com isso, confere essa dica que vai te salvar no cálculo da área entre curvas:
- No cálculo da área A, quando temos duas funções, o módulo |f(x)-g(x)| deve ser pensando assim A função que está superior menos a função que está abaixo.
Por exemplo, veja na Figura 2. O gráfico de g(x) = x está acima de f(x) =x², portanto, o integrando será: |f(x)-g(x)| = x-x². Com isso, vamos as contas:
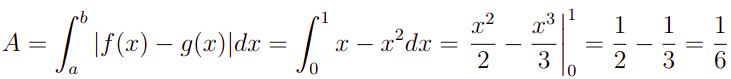
E a área desejada fica calculada.
Um exemplo sem limites de integração dados
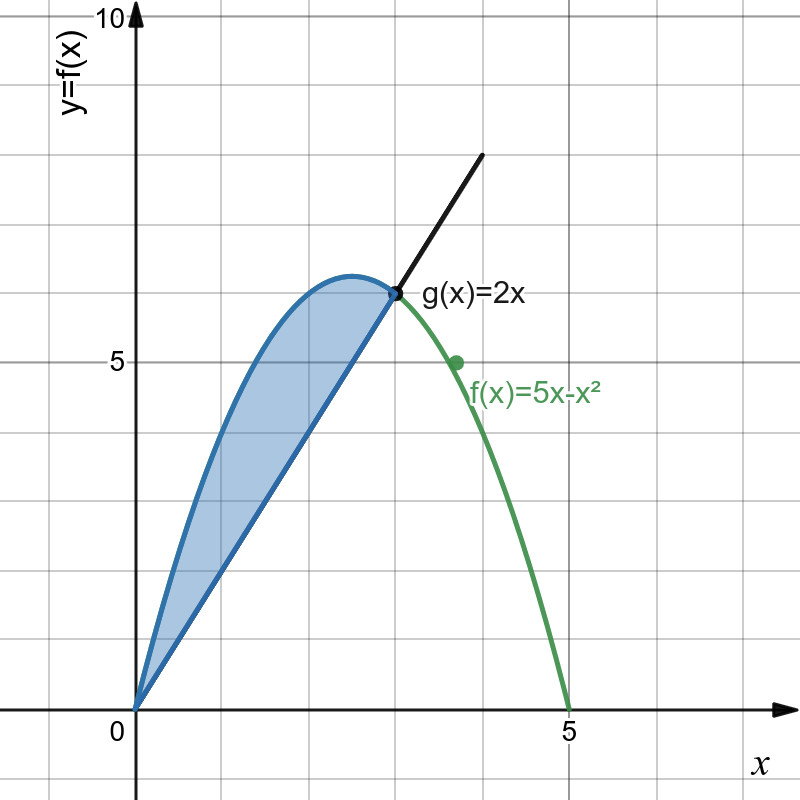
Por fim, vamos determinar a região entre as curvas y=2x e y=5x-x². Isso mesmo, dessa vez eu não te dei os limites a e b. Mas calma gurunauta, eu estou aqui pra te ajudar e não complicar sua vida. Então, vamos calcular esses limites, para isso, segura essa dica:
- Para determinar os limites de integração entre duas curvas basta que você determine os pontos de intersecção entre elas.
Ou seja, devemos achar os x tais que y=2x e y= 5x-x² sejam iguais. Então, igualando essas expressões temos:

Logo, a= 0 (menor limite de integração) e b= 3 (maior limite de integração). Além disso, empregando a regra que usamos anteriormente, o módulo do integrando é |f(x)-g(x)| = (5x-x²) – (2x), basta conferir o gráfico das funções na Figura 3.
Portanto, obtemos que a área A é calculada da seguinte forma:
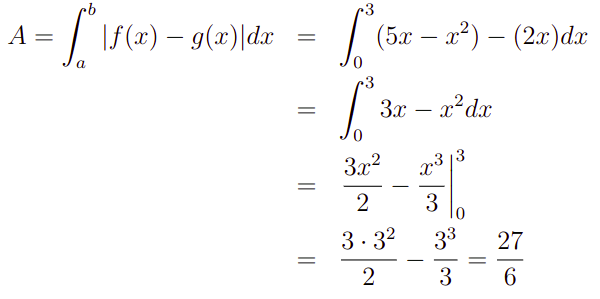
Com isso, o problema fica resolvido.
Além disso, se você quiser gerar gráficos para estudar as funções e visualizar melhor os desenvolvimentos ao longo dos seus estudos confere o artigo gráficos, vai te ajudar bastante gurunauta.
E claro, lembra sempre de contar com a MeuGuru para impulsionar seus estudos e garantir sua aprovação e riscar de vez a palavra reprovação do seu vocabulário. Até mais!.





