Nesse artigo, vamos ver como resolver equações diferenciais ordinárias de 2º ordem.
No estudo das equações diferenciais, após estudarmos as equações de primeira ordem chegamos a um dos pontos mais importantes: as equações de 2º ordem. De fato gurunauta, esse assunto é um assunto quente na disciplina de EDO tanto por relevância nas ciências quanto na matemática. Portanto, não tenha dúvidas, na sua prova você irá ter que resolver alguma equação de 2º ordem. Então, vem comigo que vou te ajudar nessa jornada.
As equações diferenciais ordinárias de segunda ordem
Primeiro de tudo, vamos entender o que são essas equações. A ideia segue a mesma linha das equações de primeira ordem. Em linhas gerais, nossa equação possuirá uma função incógnita x=x(t) associada a uma derivada segunda, ou derivada de ordem 2/segunda ordem. Assim, a expressão abstrata para essas equações pode ser posta da seguinte forma

onde a variável independente é t. No entanto, a forma abstrata não nos ajuda muito a entender e conhecer essas EDOs. Na verdade, vamos estar interessados no caso em que as equações de segunda ordem são lineares. Nesse sentido, vamos a essas formas.
Forma geral das equações diferenciais 2º ordem lineares
Uma equação diferencial de segunda ordem linear tem a seguinte forma geral
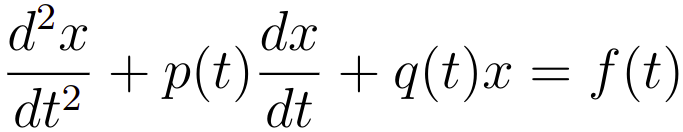
onde p(t), q(t) e f(t) são funções contínuas. Se a função f(t) diferente de 0 a EDO é dita não homogênea. Por outro lado, caso f(t) = 0 a EDO é dita homogênea.
Equações diferenciais de 2º ordem com coeficientes constantes
Um caso interessante ocorre quando as funções p(t) e q(t) são constantes. Na verdade, esse talvez seja um dos casos mais frequentes das EDOs de segunda ordem. Sob essa hipótese a EDO passa a ser a seguinte

em que a deve, obrigatoriamente, ser não nula e b, c são constantes reais.
Tendo em mãos o conhecimento sobre essas equações diferenciais. Podemos, passar para os métodos de solução.
Como resolver as EDOs de 2º ordem lineares
Agora, vamos ver como resolver as EDOs de segunda ordem lineares. Todavia, vamos nos formar na parte homogênea apenas, de fato, resolver uma EDO não homogênea é algo que precisamos de um pouco mais de espaço. Dito isso, vamos conhecer, primeiro, o princípio da superposição.
O princípio da superposição para soluções de uma EDO de 2º ordem
As EDOs de segunda ordem possuem duas soluções. Em verdade, isso é muito bem justificado pela álgebra linear, no entanto, aqui não vou entrar nesses detalhes. O que você precisa saber é que toda EDO de segunda ordem linear possui duas soluções linearmente independentes e a solução geral é uma combinação linear dessas. Isto é, se x_1 e x_2 resolvem a EDO homogênea de segunda ordem, segue que a solução geral é

Logo, todos os métodos abaixo que vamos mostrar acabam nos levando a duas soluções que serão linearmente independentes.
Como resolver: Caso geral e linear
O caso geral não possui uma forma explícita e/ou método universal para ser solucionado. No entanto, há métodos que usam aproximações para garantir tal solução. No método de Frobenius a solução toma a forma:

Já no método das séries de potência

onde c_n é uma constante real e x_0 é um número real onde, é usado como aproximação dos valores de t.
Como resolver: Coeficientes constantes
No caso dos coeficientes constantes, há uma forma de termos soluções explícitas para as EDOs. Em verdade, esse método é guiado pela ideia de supor que a solução da parte homogênea da EDO é da seguinte forma:


ou seja, o problema agora passa a ser resolver uma equação do segundo grau e, bem, esse problema você sabe resolver. Com isso, você verá que teremos, naturalmente, duas soluções e elas formarão a solução completa da parte homogênea da seguinte forma

onde A e B são constantes. Ou seja, a solução é a combinação linear das exponenciais dos autovalores.
Aqui é importante dizer que os lambdas podem nos guiara a alguns casos específicos:
- Se os lambdas são diferentes, a solução está completa e dada conforme x_h acima.
- Se os lambdas são iguais há apenas uma solução e você deve encontrar outra solução através de outro método. Esse caso, merece um artigo especial pois nos levará ao método da variação dos parâmetros.
- Os lambdas podem ser complexos e nossa exponencia se torna proporcional a uma soma de senos e cossenos.
Espero que você tenha curtido o artigo gurunauta. E lembre-se, qualquer coisa conte com a MeuGuru que te ajudamos a salvar esse semestre em caos.





