Como resolver Integrais com frações parciais

Fala gurunauta, nesse artigo você vai ver como resolver integrais com frações parciais. Em geral, nos cursos de cálculo integral somos apresentados a diversos métodos para resolver certos tipos de integrais. Em particular, um desses métodos é usado para integrandos do seguinte tipo

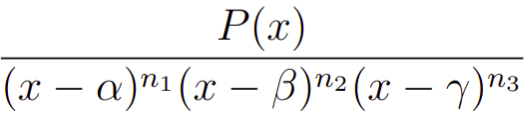
onde P(x) é uma função polinomial e n₁, n₂ e n₃ são números inteiros. Integrais desse tipo de funções as vezes são complicadas num primeiro olhar. Todavia, vamos ver que o método da decomposição em frações parciais permite que esse tipo de integral seja essencialmente simples. Então, cola comigo gurunauta que hoje vamos aprender o método da decomposição em frações parciais.

A decomposição em frações parciais

Agora, vamos nos ater a entender o método por trás das frações parciais. Em geral, nossa ideia aqui será desenvolver um método que torna a Expressão 1 algo mais simples, podemos até dizer, mais amigável. Nesse sentido, vamos considerar dois tipos de integrandos. Primeiramente, vamos ao tipo 1 de integrando que é o seguinte

onde P(x) é um polinômio. Ademais, também consideraremos outra forma que é o tipo 2 dado a seguir

onde, é inserimos mais um termo no denominador. De posse disso, vamos agora ver como essas frações podem ser decompostas em termos elementares.

Frações do tipo 1 – como resolver

Estabeleceremos essa primeira decomposição através de um Teorema. Entretanto, antes disso é importante convencionarmos uma forma particular para P(x), essa será a seguinte.

Com isso, vamos enunciar o Teorema que guiará a forma das nossas decomposições.

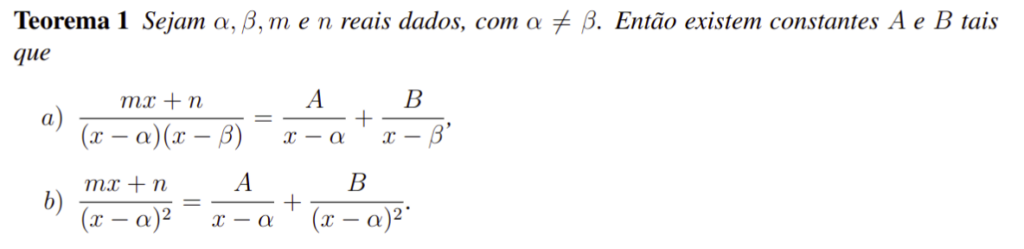
De fato, ter as decomposições do Teorema 1 em mente será muito importante para que nós possamos avaliar essas integrais. Decerto, com ele em mãos, nosso trabalho será unicamente determinar as constantes A e B das expressões acima.

Frações do tipo 2 – como resolver

Por outro lado, para a fração do Tipo 2 e considerando P(x) como

Tendo isso em vista, podemos enunciar um poderoso Teorema que guiará nossas decomposições. Com efeito, esse é exposto logo a seguir

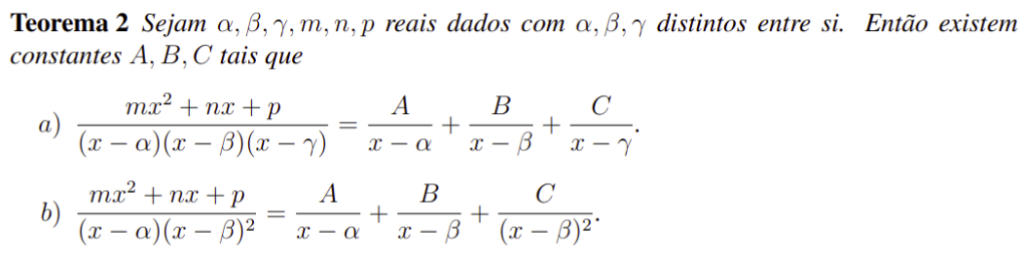
Integrais com frações parciais

Uma vez que temos o entendimento teórico das decomposições de frações parciais, podemos então praticar esse assunto. Decerto, agora veremos dois exemplos resolvidos para cada tipo de integral.

Como resolver integrais com frações parciais do tipo 1

Primeiramente, vamos apresentar o problema. Aqui, nosso objetivo será resolver a seguinte integral

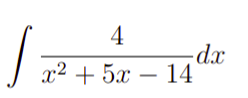
Vamos exibir o passo a passo desse desenvolvimento. Com efeito,

De posse disso, vamos determinar A e B resolvendo o sistema linear a seguir, o qual é obtido por igualdade polinomial

Dessa forma, conseguimos chegar ao nosso objetivo. Viu só gurunauta, o processo torna-se essencialmente simples uma vez que chegamos a integrais elementares.

Como resolver integrais com frações parciais do tipo 2 – Faça você mesmo!

Como você viu, as ideias e os Teoremas são muito similares gurunauta. Tendo isso em vista, agora é sua hora de por o conhecimento em prática. Nesse sentido, que tal encarar nosso desafio, nada de outro mundo beleza?, basta resolver a seguinte integral

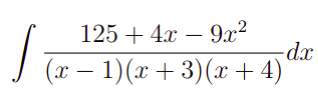
Mas calma, vou te dar umas dicas, por que aqui estamos preocupados com seu aprendizado. Primeiro, você terá que usar a decomposição do item (a) do Teorema 2 e deverá chegar no seguinte resultado

Ou seja, as constantes serão 6, -8 e -7. Por fim, a resposta final que com toda certeza você irá obter será

E lembre-se, para quaisquer perrengues universitários saiba que na MeuGuru temos um Guru especial para te ajudar com seus trabalhos.