O divergente é um dos operadores diferenciais mais importantes quando entramos no cálculo de funções de várias variáveis. Não apenas isso, mas o conceito de divergente urge já nos cálculos iniciais. Em suma, nós somos apresentados a esse operador como uma nova forma de calcularmos derivadas. Por outro lado, além da relevância matemática, esse operador passa a ser interessante por suas inúmeras aplicações para o tratamento de funções de várias variáveis.
Tendo isso em vista, nós da MeuGuru preparamos um texto especial para você, onde vamos abordar o que é esse operador e ainda apresentaremos exemplos resolvidos.
O que é o operador divergente
O operador divergente é um conceito importante na matemática e na física que é usado para descrever a expansão ou contração de um campo vetorial em um determinado ponto. Ele é um operador diferencial vetorial e é denotado pelo símbolo.

Em três dimensões, a definição do operador divergente é a soma das derivadas parciais das componentes do campo vetorial em relação a cada coordenada. De forma matemática, o operador divergente é expresso pela seguinte fórmula.
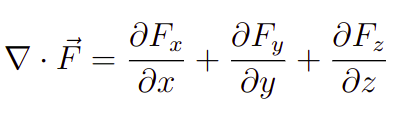
Onde, o campo vetorial tridimensional tem componentes Fx , Fy e Fz $F_x$, $F_y$, e nas direções dos eixos x, y e z, respectivamente. Por outro lado, em duas dimensões, a definição do operador divergente é semelhante, mas com apenas duas coordenadas isto é

Comentário sobre aplicações
O operador divergente tem diversas aplicações em áreas como física, engenharia e ciências ambientais. Em particular, podemos citar algumas dessas aplicações. Com feito, na física, ele é usado para calcular fluxo e analisar conservação de massa e a lei de Stokes. Por outro lado, nas engenharias vemos que esse operador é empregado para a análise de estruturas e cálculo de forças internas.
Ademais, quando olhamos para as ciências ambientais, obtemos algumas aplicações muito interessantes. Em particular, nesse contexto, o operador divergente pode ser empregado para modelar o movimento de poluentes e analisar a qualidade do ar e da água.
Exemplos resolvidos
Agora, sabendo a definição do operador divergente podemos então passar a praticar esse assunto. Com efeito, vamos fazer o desenvolvimento passo a passo de dois problemas.
Divergente de um campo vetorial de duas componentes
Primeiramente, vamos considerar um campo vetorial de duas componentes, isto é.
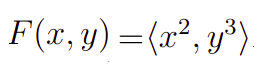
Com isso, vamos calcular o divergente desse campo vetorial. Para tanto, usando a definição mostrada anteriormente teremos que o passo a passo desse desenvolvimento pode ser feito calculando as derivadas parciais acima separadamente, ou seja, teremos que
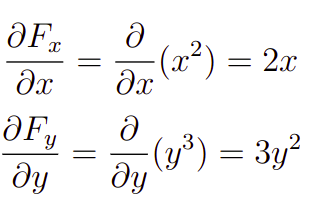
Portanto, com isso obteremos, finalmente, o seguinte resultado.
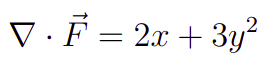
Divergente de um campo vetorial de três componentes
Agora, vamos resolver um problema similar, porém, nesse caso teremos três componentes no nosso campo vetorial. Agora, consideremos o problema para o dado campo
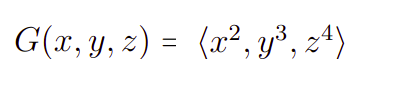
Então, o cálculo do divergente de G é feito, passo a passo, da seguinte forma
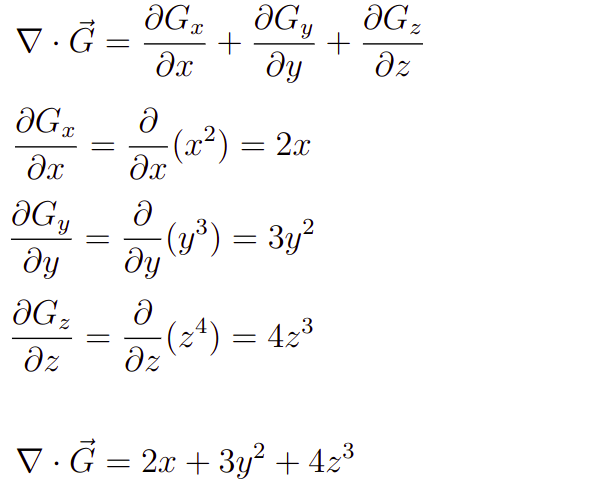
e assim fica resolvido o problema.





