Confira nesse artigo, um resumo com exercícios resolvidos sobre energia mecânica para você arrebentar na sua prova de física.
Energia mecânica o que é?
Nada mais justo do que começarmos o texto buscando entender o que é essa energia. Deuqe fato, a energia mecânica é o tipo de energia que aparece em sistemas mecânicos, isto é, em situações físicas governadas pelas leis da mecânica de Newton. Ou seja, ela aparece ao longo de todo o estudo da mecânica e da física 1.
Além disso, a energia mecânica mede a capacidade de um corpo em realizar trabalho mecânico. Isto é, se um corpo possui mais energia mecânica ele terá maior chance de conseguir realizar trabalho.
Ademais, esse tipo de energia se subdivide em dois tipos: potencial e cinética. Assim, essa energia, em suma, é constituída de uma soma dessas duas energias, tendo que sua fórmula é
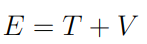
onde T é a energia cinética e V a energia potencial. No entanto, há sistemas que podem ainda estar dissipando energia, seja por algum tipo de atrito ou similar, nesse caso a fórmula para E é dada por
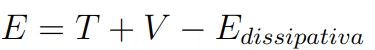
onde o último termo é a quantidade de energia que é dissipada no sistema.
Os sistemas em que não há dissipação de energia são muito importantes na física. Em verdade, esses são chamados de sistemas conservativos e neles dizemos que a energia mecânica é conservada. Entretanto, deixaremos esse papo sobre conservação de energia para outro artigo, agora, vamos ao resumo dos dois tipos de energia mecânica: a potencial e cinética.
Energia Mecânica potencial: resumo e fórmulas
A energia potencial, ou simplesmente chamada de potencial, é um tipo a energia que aparece em decorrência das forças que agem no sistema. Portanto, a energia potencial depende do tipo de força, logo, há uma infinidade de fórmulas possíveis para a energia potencial. No geral, denotamos ela por
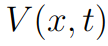
e ela representa o trabalho executado por uma força que está agindo num corpo qualquer.
No entanto, no caso em que o sistema é conservativo podemos expressá-la através do campo de forças F que age no sistema. Nesse caso, temos que o potencial fica definido pela seguinte fórmula
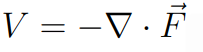
ou seja, é menos o gradiente da força F associada. Mas calma gurunauta, vamos utilizar essa fórmula apenas em exercícios e estudos mais avançados.
Agora, vamos apresentar duas fórmulas específicas do potencial V. Essas fórmulas são os potenciais associados a força peso e força elástica. A primeira é o potencial gravitacional dado por
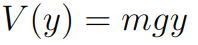
onde, g é a aceleração da gravidade, m é a massa do corpo e y a distância até o solo que o corpo está. Além dessa, vamos apresentar o potencial associado a força elástica que é
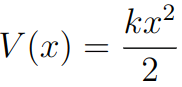
onde, k é a constante de elasticidade da mola e x é a elongação ou compressão da mola.
Energia Mecânica cinética: resumo e fórmulas
Agora, vamos estudar sobre a energia cinética. Diferentemente da anterior, a energia cinética não é associada a forças, na verdade, ela é associada apenas ao movimento dos corpos. Isto é, essa energia vem da velocidade que os corpos possuem.
Sendo assim, a media dessa energia nos diz como corpos podem variar suas posições. Além disso, por não se associar a um tipo específico de força, a energia cinética é mais geral. Portanto, calcular essa energia é bem mais simples, na verdade, há uma fórmula geral para isso que é a seguinte
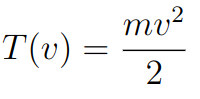
onde, m é a massa do corpo e v é sua velocidade. Com isso, ter o conhecimento da massa e velocidade permite-nos a conhecer a anergia cinética de um corpo. Ademais, essa energia é muito importante na física e não apenas em mecânica, de fato, ela motivou os estudos para a criação da chamada teoria cinética dos gases.
Exercícios resolvidos
Com o conteúdo na ponta da língua, resta agora por a mão na massa e praticar. Então, vamos aos exercícios resolvidos
Exercícios resolvidos teóricos
Questão 1) É correto afirmar que a energia mecânica num sistema é sempre a soma das energia potenciais e cinéticas ?
Resposta: Não, pois em sistemas que possuem dissipação de energia a energia mecânica total é menor que a soma das componentes cinéticas e potenciais.
Questão 2) A energia potencial pode ser maior que a energia mecânica?
Resposta: Não, na verdade, tanto a energia cinética quanto potencial nunca poderão ultrapassar o valor da energia mecânica. No entanto, em sistemas conservativos pode haver pontos específicos em que a energia mecânica, alí, seja igual a energia potencial ou cinética.
Exemplos resolvidos com fórmulas
Para praticar, vamos calcular a energia mecânica de um corpo de 10kg que cai de uma altura y=h = 10m (considere o sistema conservativo). No início do trajetória, o corpo está parado, logo sua energia cinética é nula, portanto, T =0, então, a energia mecânica será totalmente de origem potencial gravitacional, ou seja, teremos que
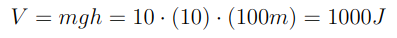
Logo, E = T+V = V = 1000j. Ademais, podemos ainda calcular a energia cinética no ponto mais baixo (h=0) sabendo que o corpo toca o solo com velocidade v = 10(2)^{1/2}m/s (10 vezes raíz de 2). Então, teremos que a energia cinética é
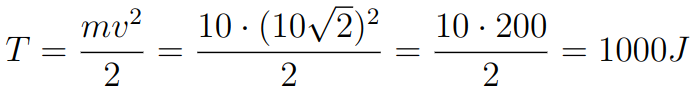
E é isso gurunauta, espero que tenha gostado do texto e lembre-se de contar com a MeuGuru para te ajudar nos estudos e garantir a aprovação no semestre.





