Fala gurunauta, nesse artigo vamos falar sobre as equações diferenciais ordinárias, de segunda ordem, não homogêneas. De fato, nós já falamos sobre as equações diferenciais de segunda ordem, todavia, nós restringimos as formas de solução a um tipo específico de EDO: homogêneas. Tendo isso em vista, agora vamos focar em entender o caso não homogêneo. Particularmente, nos ateremos ao método dos coeficientes a determinar que pode ser uma ótima carta na sua manga na hora de resolver aquela prova de EDO gurunauta.
Apresentando o problema
Então gurunauta, nosso contexto será trabalhar encima do seguinte tipo de EDO:
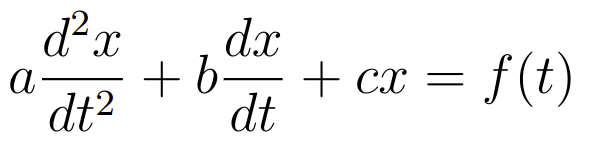
onde a, b e c são constantes e a é não nulo. Ademais, a função f(t) é uma função suave que depende unicamente da variável independente t. Esse problema, consiste numa extensão do trabalhado no artigo. Decerto, a ideia geral para resolver esse tipo de problema pode ser posto nas seguintes etapas
- Etapa 1. Resolver o problema homogêneo conforme discutido aqui. Isso dará uma solução xh.
- Etapa 2. Resolver o problema particular associado para o tipo específico da função f(t). Isso dará uma solução xp.
- Etapa 3. A solução geral da EDO será uma solução x que é soma das soluções obtidas na Etapa 1 e Etapa 2. Isto é, x(t) = xh + xp.
Entretanto, o problema do roteiro acima está, exatamente, na Etapa 2. De fato, não se há um método que garanta uma solução para qualquer tipo de função f(t). Porém, é conhecido que para alguns tipos específicos de funções é possível ter uma boa estimativa de solução particular, o qual exploraremos a seguir.
Equações diferenciais de 2º ordem: O método dos coeficientes a determinar
Tendo em vista a apresentação do problema anterior, vamos, agora atacar o problema para alguns casos de funções f(t). Nesse método, a ideia geral consiste em construir uma solução particular que resolva o problema da EDO para f(t) do seguinte modo.
- Passo 1. Chutamos uma solução particular associada a um coeficiente constante que será determinado.
- Passo 2. Levamos a solução na nossa EDO.
- Passo 3. Determinamos o coeficiente constante de modo que a igualdade com a função seja satisfeita.
Ou seja, o problema torna-se essencialmente uma conta de substituição na EDO. Todavia, esse método funciona apenas sob algumas funções, em verdade, podemos relacionar essas funções bem como a forma das soluções particulares conforme a Tabela 1 a seguir.

Além disso, há uma ressalva a ser feita nesse método. Caso, a função f(t) coincida com alguma das soluções da parte homogêna da EDO, a forma da solução particular deve ser txp.
Resolvendo um exemplo passo a passo
Vamos resolver a seguinte EDO
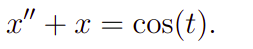
Com efeito, usando os métodos já conhecidos você pode verificar que a solução homogênea é a seguinte
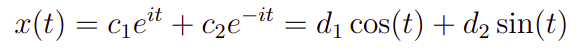
Agora, vamos obter uma solução para a parte não homogênea. Para tanto, consultando a Tabela 1 e a observação feita posteriormente, teremos a seguinte forma da solução particular
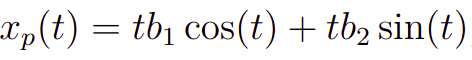
em que suas derivadas são

então, levando essas funções na EDO obteremos que

usando a igualdade dos termos é possível obtermos o seguinte sistema linear

e assim, fica determinado que

Ademais, a solução particular então pode ser expressa por

Além de que, a solução geral da EDO fica então dada por
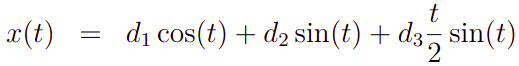
Com isso, chegamos ao fim de mais um texto gurunauta. E lembre-se, sempre conte com MeuGuru para te ajudar nos perrengues universitários.





