Fala gurunauta, nesse artigo vamos falar sobre as equações diferenciais ordinárias separáveis.
Continuando no assunto das equações diferenciais ordinárias, vamos agora estudar as equações separáveis. Decerto, as equações diferenciais separáveis são muito frequentes nos primeiros cursos EDOs. Portanto, saber identificar e resolver esse tipo de equação pode garantir para você uma ótima nota na sua prova e, desde já, te salvar da chance de ir para as provas finais.
O que são Equações diferenciais ordinárias separáveis
Primeiro de tudo, vamos entender o que são equações diferenciais ordinárias separáveis. No artigo, de EDOs de primeira ordem vimos uma forma geral para essas equações. Em linhas gerais, a derivada total da função incógnita era igual a uma função bem arbitrária que definiria a forma da equação, conforme a seguir
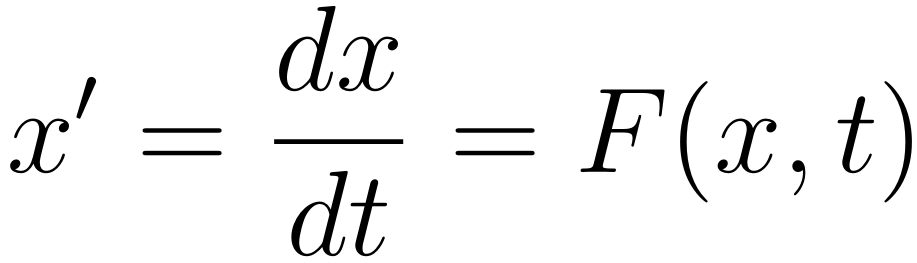
De fato, a função F(x,t) pode ser bem arbitrária, logo, podendo levar a expressão acima a equações muito complicadas. Mas, agora, vamos imaginar que a forma da função F(x,t) seja um pouco mais específica, em verdade, uma divisão de uma função f(t) e uma função g(x). Sob essa condição, a equação anterior pode ser escrita da seguinte forma

lembre-se que g(x) deve ser não nula no domínio que está definido. Ou seja, a dependência das variáveis dependentes e independentes fica totalmente separada nas funções f(t) e g(x). Quando isso ocorre, temos dizemos que a equação diferencial ordinária é uma equação separável. Essas equações podem ser facilmente resolvidas, decerto, muitas vezes já resolvemos essas equações nos primeiros cursos de Cálculo.
Como resolver EDOs separáveis
Agora que você sabe identificar uma equação separável, vamos ver com resolver essas EDOs. Aqui, de antemão, é necessário dizer que nossos objetivos são práticos, logo, abriremos mão do rigor matemático. Feito essa consideração, vamos exibir um método que funciona e podemos obter a solução x(t), com efeito, consideremos a EDO

Vamos aplicar o procedimento de separação de variáveis. Esse método consiste em separar as funções e diferenciáveis de cada lado da igualdade, da seguinte maneira
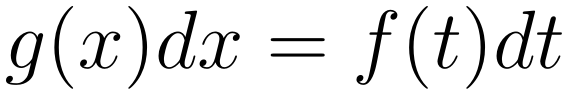
tendo separado as variáveis, podemos então simplesmente integrar de ambos os lados, do seguinte modo

Com isso, podemos simplesmente transladar o problema de uma EDO separável para a resolução de duas integrais de uma variável. Agora, para fixar as ideias, vamos a um exemplo
Exemplo resolvido de uma EDO separável
Consideremos a seguinte EDO.

Veja que ela pode ser separável, de modo que pelo método de separação de variáveis teremos o seguinte

Agora, vamos fazer o passo a passo do desenvolvimento seguinte. Bom, integrando de ambos os lados segue que

e assim a solução x(t) fica determinada.
E Lembre-se de contar sempre com a MeuGuru para te ajudar e te salvar da reprovação.





