Estequiometria – Aplicando regra de três – Matemática básica 1.1

A estequiometria é um dos assuntos mais cobrados em vestibulares na área de química. Certamente, esse conteúdo é algo que tira o sono de muitos vestibulandos e de ingressantes em cursos da área das ciências exatas visto sua dificuldade tanto por conta de cálculos como também pelo entendimento teórico dos problemas. Uma vez que, a determinação correta dos cálculos é intimamente ligada com a proporcionalidade de aspectos determinados pelo processo/reação química que analisamos.

Nesse sentido, nós da MeuGuru decidimos trazer esse artigo especialmente para você sendo que esse é o artigo 1.1 da série de matemática básica que nós decidimos iniciar aqui no blog. Com efeito, nesse artigo te mostraremos que a estequiometria que, apesar de ser um assunto visto em química não passa de uma mera aplicação de regras de três simples que já falamos em nosso primeiro artigo da série. Então, vem com a gente gurunauta que hoje vamos aplicar nossos conhecimentos em um tema quente e bem interessante que é a estequiometria química com regras de três simples.

Estequiometria – Entenda o princípio básico

Antes de tudo é necessário entendermos um pouco dos fundamentos que perpassam a estequiometria e o cálculo estequiométrico. Em suma, a química e todo o funcionamento de processos químicos são regidos por equações químicas muito bem conhecidas e fundamentadas, ademais, essas equações seguem ainda leis as quais são ditas pela nossa natureza e assim permitem que a realidade observável que conhecemos exista.

Leis químicas importantes

Há então algumas leis que nós precisamos que você tenha em mente quando você for estudar química e/ou estequiometria, sendo essas.

• Com efeito, a primeira dessas é a Lei de Conservação da Massa (Lei de Lavoisier) a qual afirma que a massa total dos reagentes em uma reação química é igual à massa total dos produtos. Em outras palavras, a massa é conservada durante uma reação química.
• Ademais, temos a Lei das Proporções Definidas (Lei de Proust) que de acordo com essa lei, uma substância pura sempre conterá os mesmos elementos em proporções definidas em massa. Isso significa que a relação entre as massas dos elementos em um composto químico é constante.
• Segue ainda a Lei das Proporções Múltiplas (Lei de Dalton) que afirma que, quando dois elementos formam mais de um composto, as massas de um desses elementos em cada composto podem ser expressas como uma razão de números inteiros simples.
• Por fim, e muito importante há ainda a Lei de Avogadro a qual estabelece que volumes iguais de gases, nas mesmas condições de temperatura e pressão, contêm o mesmo número de moléculas. Isso significa que os gases se combinam em proporções de volume que são expressas por números inteiros simples.

Explicação das leis químicas

As leis químicas que estabelecem que o funcionamento das reações foram obtidas a partir da observação e experimentação. Assim, essas leis tem implicações extremamente importantes e relevantes para nosso universo como um todo em particular essas leis estabelecem proporções para quais reações químicas acontecem. Com efeito, vamos destacar um pouco essas leis.

A primeira dessas nos traz a conservação da massa. Dessa forma, vemos que ao considerarmos todos os elementos, reagentes e produtos em um processo/reação química não teremos perca de massa e logo a massa será conservada. Dessa forma, as massas dos reagentes e produtos poderão ser postos como elementos de proporcionalidade conforme dito na segunda lei.

Por conseguinte, temos a terceira lei a qual nos dá um parâmetro de números inteiros que associam a razão de massas. Em particular, essa razão de massas é na verdade o que chamamos de mol, número de mol ou mesmo moles (conforme português de Portugal).

Por fim, temos a quarta e última lei que é lei de Avogadro garante a existência dos coeficientes estequiométricos que são os números inteiros que permitem que cada reagente envolvido se relacione com os outros de forma a produzir produtos da reação de forma bem definida e proporcional.

Logo, todas essas proporções bem estabelecidas formam um ambiente perfeito para a aplicabilidade de regras de três simples quando nos limitamos a apenas duas grandezas físicas de interesse. Decerto, veremos a seguir algumas relações de proporcionalidades na química em processos / reações químicas e como elas estão bem definidas e associam-se entre sí.

Relações de proporção na estequiometria

Então, com intuito de entendermos claramente o que são as quantidades envolvidas em processos químicos vamos esquematizar um processo químico através de uma reação. Nesse sentido, vamos tomar uma equação simples como exemplo a qual apresentamos a seguir.

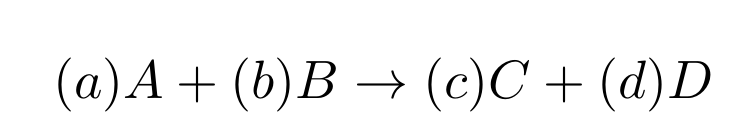
Em certo, essa equação é bem geral e os coeficientes dela são os apresentados em minúsculo entre parênteses. Ademais, a partir das leis de conservações que vimos anteriormente podemos garantir que os coeficientes estequiométricos acima garantem a proporcionalidade dos reagentes e produtos bem como com relação a suas massas e consequentemente volumes e disso segue que estabelecemos para qualquer uma das quantidades q (onde q é o rótulo para os elementos arbitrários A, B, C e D) da seguinte forma

onde 6.63×10^-23 denota o número de Avogadro que diz que em 1 mol de qualquer espécie química há, em média 6.63×10^-23 átomos e 22.7 é a quantidade de volume vq da espécie q, nq é o número de mol, e Mq é a quantidade de massa da espécie q.

Então, de posse disso podemos com essas relações em mente realizar várias contas e desenvolver diversas questões envolvendo estequiometria e processos de cálculo estequiométrico. Nesse sentido, a seguir te mostraremos como resolver passo a passo um problema desse tipo.

Exercício resolvido com cálculo estequiométrico passo a passo

Bom, agora chegou a hora da gente praticar então vamos ver um exercício passo a passo que caiu na prova da FUVEST esse exercício é o seguinte.

(FUVEST) Considere a transformação de ozônio em oxigênio comum representada pela equação:
2O₃ -> 3 O₂.
Determine a massa de oxigênio produzida quando 96 g de ozônio se transformam completamente. (Dada a massa atômica: O = 16 u)

Em suma, nosso interesse é usar regra de três simples para resolvermos esse problema. Então, veja que que como dado a massa atômica do oxigênio é 16u e queremos determinar a massa de oxigênio produzida a partir da massa de ozônio. Nesse sentido, temos uma relação de proporcionalidade envolvendo massa do reagente e massa do produto e logo devemos determinar primeiro a relação que nos dá a proporção fixa e conhecida a qual é dita pela equação e dela temos que 2 mols de ozônio que tem massa 16*3 = 48 u produz 3 mols de oxigênio que tem massa 16*2 = 32. Dessa forma, segue que o cálculo aqui será o seguinte:

daí temos então 96/96 = 96/x => x = 96g e haverá produção de 96 gramas de oxigênio note que esse exemplo mostra a exata conservação da massa conforme tínhamos mostrado como lei.

Referências

1. IEZZI, Gelson; DOLCE, Osvaldo; DEGENSZAJN, David; PÉRIGO, Roberto. Fundamentos da Matemática Elementar: Volume Único. São Paulo: Atual, 2019.
2. GIOVANNI, José Ruy; CASTRUCCI, Benedito; GIOVANNI JR., José Ruy. A Conquista da Matemática: Volume Único. São Paulo: FTD, 2018.
3. DANTE, Luiz Roberto. Matemática Contexto & Aplicações: Volume Único. São Paulo: Ática, 2019.
4. GOMES, José Ruy; MACHADO, Antônio dos Santos; LOPES, José Lellis. Matemática: Paiva para o Ensino Médio. São Paulo: Moderna, 2019.
5. BONJORNO, José Roberto; GIOVANNI, José Ruy. Matemática Fundamental: Uma Nova Abordagem. São Paulo: FTD, 2018.
6. Khan Academy. Estequiometria. Disponível em: https://pt.khanacademy.org/science/chemistry/chemical-reactions-stoichiome. Acesso em: 12 jan. 2024.
7. ANTON, Howard; RORRES, Chris. Álgebra Linear com Aplicações. Porto Alegre: Bookman, 2012.
8. STEINBRUCH, Alfredo; WINTERLE, Paulo. Geometria Analítica. São Paulo: Pearson, 2009.
9. FLEMMING, Diva Marília; GONÇALVES, Miriam Buss. Cálculo II: Funções de Várias Variáveis. São Paulo: Pearson, 2013.