Fala gurunauta, hoje vamos falar sobre Física estática. Na verdade, vamos resolver, juntos, um problema em apenas 4 passos. De fato, a parte da estática na física é muito
Entenda o que é a estática física
A estática representa um estado específico de um corpo de acordo com as leis de Newton. Em particular, esse estado é caracterizado quando a resultante de todas as forças que agem em um corpo é nula.
Ademais, esse estado é especialmente interessante por representar diversas situações cotidianas em nossa realiade. Logo, entender problemas básicos de estática torna-se fundamental para aplicações diretas em problemas de engenharia, com destaque a engenharia civil.
Além de que, esses problemas ainda permitem um bom treino e aperfeiçoamento das leis de Newton. Tendo isso em vista, vamos agora entender todo o passo a passo de como resolver um problema de estática extremamente geral.
Apresentando o problema
Feita as devidas apresentações da relevância da estática, vamos apresentar o problema que estudaremos. Com efeito, consideraremos um corpo de massa m que é suspenso por um fio vertical (eixo y) que é ligado a dois fios inclinados conforme Figura 1.
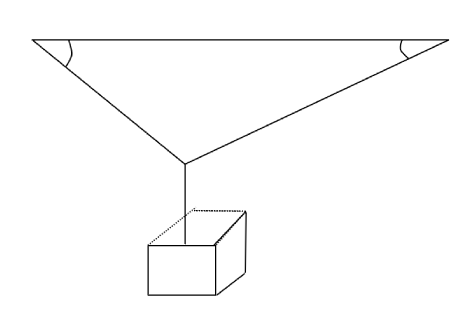
De posse disso, determine as intensidades das trações nos fios inclinados, uma vez que, a configuração do problema da Figura 1 pode ser expressa conforme Figura 2.

Ademais, veja que, o problema deve ser resolvida em termos dos ângulos alfa e beta.
Resolvendo o problema de estática física
De posse do problema anterior, bem como da Figura 2, vamos resolver esse exercício passo a passo. Para tanto, seguiremos uma abordagem sequencial, onde, em cada tópico abaixo iremos fazer parte da solução do problema. Portanto, vamos a essas etapas.
Passo 1 – Desenhando as forças
De início, vamos começar a resolver o problema desenhando as forças que agem no corpo. Dessa forma, obteremos o seguinte diagrama de forças.

Em que, realizamos a decomposição das forças T1 e T2, uma vez que, essas forças ficam inclinadas em relação ao plano. Por conseguinte, elas agem no corpo em ambos os eixos, assim, sendo necessário decompô-las para uma análise com uso das leis de Newton.
Passo 2 – Aplicando a condição de estática física
Agora, tendo em mãos a Figura 3, vamos aplicar a condição de estática. De fato, essa condição advêm da segunda lei de Newton conforme ja mencionado anteriormente. Todavia, aqui aplicaremos ela duas vezes, uma para cada um dos eixos coordenados, isto é, o eixo x e o eixo y. Com efeito, teremos as seguintes equações:

Passo 3 – Obtendo um sistema de equações
De posse da expressão 1, podemos desenvolver as trações decompostas de modo a termos um sistema de equações que associem as quantidades físicas desejadas. Para isso, necessitaremos usar a geometria do problema físico, com efeito, veja que podemos obter o seguintes triângulos para as trações
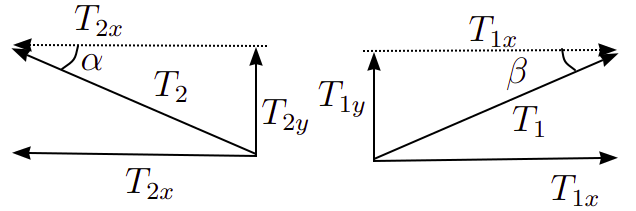
Com isso, podemos usar as relações trigonométricas no triângulo retângulo para termos o seguinte
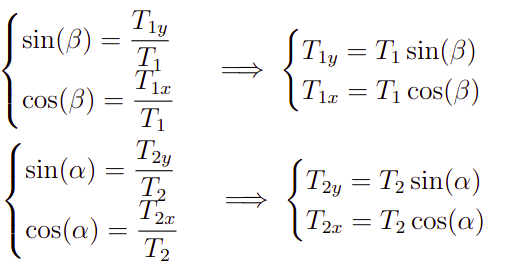
Com isso, podemos levar os resultados da Expressão 2 na Expressão 1 de modo a obtermos o seguinte sistema de equações.
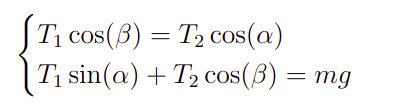
Então, o problema em sí torna-se, agora, resolver o sistema dado na Expressão 3 para T1 e T2.
Passo 4 – Resolvendo o sistema
Por fim, vamos resolver o sistema da Expressão 3. Para tanto, vamo primeiro isolar T1, com efeito.

Agora, levando na outra equação temos o seguinte
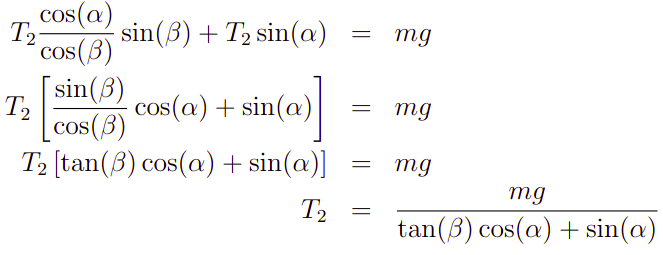
E assim, obtemos T_2. Agora, usando a expressão anterior obteremos o seguinte para T1

E T1 fica dado por.

Assim, o problema fica completamente solucionado.





