Construir gráficos de funções não é uma tarefa fácil se você não tiver uma calculadora gráfica em mãos. De fato caro Gurunauta de exatas, com toda certeza ao longo de várias provas e/ou listas de cálculo diferencial você já foi confrontado com o desafio de realizar um esboço de um gráfico de uma dada função. Certamente, essa não é uma tarefa fácil, em verdade, é uma tarefa robusta que requer a aplicação de diversas etapas de cálculo construtivas que permitem a nós ganharmos a intuição necessária para desenvolvermos tal esboço.
Nesse sentido, nós dá MeuGuru vamos ajudar você, de Exatas com esse artigo que explorará o entendimento sobre os gráficos de funções, bem como lhe ensinarão como fazê-los.
De bônus, vamos te passar um tutorial simplificado e rápido de como você poderá resolver à esses tipos de problemas.
Então, vem com a gente que hoje nós vamos nos restringir ao belíssimo mundo das aplicações de cálculo.
Por que gráficos de funções são tão importantes ?
De início, é importante entendermos o real valor de sabermos construir gráficos de funções. Decerto, gráficos de funções são representações visuais das expressões algébricas que vemos das funções.
Logo, obter e ter um gráfico lhe permitirá compreender de forma muito simples e direta o comportamento de uma determinada função matemática.
Nesse sentido, é o cálculo diferencial que fornece as bases matemáticas necessárias para que você consiga, de fato, obter esse gráfico, ou ao menos um esboço do mesmo. Decerto, é importante que você entenda que você não é, de forma alguma, um computador super incrível que é capaz de produzir gráficos de funções suficientemente sofisticadas.
Todavia, mesmo não sendo dotado de super capacidade de computação (aqui estamos nos referindo tanto no sentido de computar quanto no sentido computacional de computadores) você ainda pode obter tais noções com os métodos de cálculo.
Assim, apenas com isso já fica evidente a nós a real importância do cálculo. Entretanto, estamos ainda interessados que você gurunauta se convença de forma significativa que isso para isso, vamos explorar um pouco disso nesse tutorial que vamos realizar sobre como fazer gráficos por meio de um exemplo simples.
Tutorial: Ferramentas do cálculo para gráficos de funções
Agora, vamos começar nosso tutorial para a produção de gráficos de funções. Dessa forma, será necessário antes de tudo que você conheça as ferramentas que estão por trás disso. Com efeito, essas ferramentas são em gerais as técnicas de cálculo aprendidas em um curso de cálculo diferencial I, ou seja, estamos nos tratando de limites e derivadas. De fato, aqui sequer vamos requerer quaisquer conhecimentos sobre integrais, técnicas de integração e afins.
Em suma, a obtenção de um gráfico de uma função é feito mediante a realização de algumas etapas.
Certamente, você pode ver diferentes literaturas as quais trarão para você distintas etapas de cálculo que falarão sobre:
- Determinação das assíntotas (Estudar os limites de funções próximo a origem e suficientemente longe da origem).
- Cálculo da derivada primeira. Calcular a derivada primeira de uma função trará a você as informações necessárias para o entendimento de como a função muda em torno de determinados pontos.
- Obtenção dos pontos críticos da função. Com efeito, esses pontos críticos são, em suma, os candidatos a pontos de máximos e mínimos locais.
- Obtenção dos intervalos de crescimento e decrescimento da função a partir do estudo do sinal da derivada da função.
- Cálculo da derivada de segunda ordem. Com efeito, o cálculo da derivada segunda te permitirá computar a variação em segunda ordem da função além de permitir que você aplique o importante teste da derivada segunda que classifica os pontos críticos obtidos anteriormente em pontos de máximo e/ou mínimos.
- Estudar a concavidade da função. Em suma, o estudo da concavidade é a obtenção de intervalos da reta real onde a função é côncava para cima e/ou côncava para baixo.
Um exemplo prático passo a passo
Com a finalidade de tornarmos o guia apresentado anterior mais visual e prático vamos, agora, elaborar um exemplo sistemático desse método. Para tanto, vamos considerar um exemplo simples que trará a nós a aplicação de todos os passos e métodos acima. Com efeito, consideremos a função f(x) = x3+6x2+9 que é uma função polinomial do terceiro grau, a qual, sequer temos noção de como deve ser seu gráfico sem termos que recorrer a qualquer método computacional de análise gráfica.
Então, nesse sentido vamos as seguintes etapas que trarão a nós toda a informação sobre o gráfico dessa função
Etapa 1. Cálculo dos limites da função
De início, vamos cálculo o limite da função para quando estamos próximos a origem e suficientemente distante. Então, veja que se estivermos próximo a origem nosso valor de x torna-se pequeno, em verdade, ele será zero e logo temos que f(0) = 9. Note que aqui temos que o limite da função em zero é exatamente o valor da função nesse ponto uma vez que a função f(x) é uma função contínua.
Por outro lado, para quando temos a função distante da origem devemos considerar o valor de x se tornando imensamente grande seja positivo ou negativo. Assim, para quando x tornar-se suficientemente grande (equivalente a x tender ao infinito) e para quando x tornar-se suficientemente mais negativo (equivalente a x tender a menos infinito) teremos que
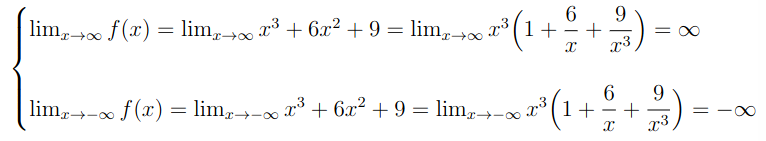
Etapa 2. Derivada da função
Agora, vamos fazer a parte da análise dos efeitos vindo da derivada da função. Com efeito, é fácil ver que sua derivada é dada por f'(x) = 3x2+12x. Ademais, vamos então obter os pontos críticos e a determinação dos seus intervalos de crescimento e decrescimento. Com efeito, veja que os pontos críticos, que são os pontos tais que “q” onde temos: f'(q) = 0 são obtidos do seguindo modo
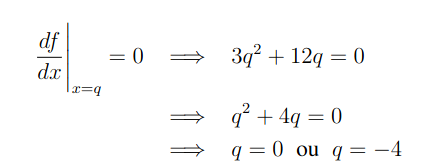
Logo, veja que temos dois pontos críticos q =0 e q =-4. Ademais, veja que esses pontos são, em suma, as raízes da função f'(x) e note que essa é uma função do segundo grau de coeficiente quadrático positivo. Logo, temos que ela é uma função de concavidade para cima, então, dentro do intervalo (-4,0) a função f'(x) é negativa e fora desse intervalo ela é positiva.
Assim, segue que a função f(x) é crescente nos intervalos onde f'(x) >0 ou seja, fora de (-4,0) e f(x) é decrescente nos intervalos onde f'(x) < 0 ou seja em (-4,0).
Etapa 3. Determinando os valores de máximo, mínimo e concavidades
Agora, passamos a analisar e estudar a derivada da segunda dessa função. De fato, você pode ver, facilmente que f”(x) = 6x + 12. Ou seja, temos uma função do segundo grau que é algo simples de ser estudado. Os pontos de máximo ou mínimo podem ser obtidos analisando os valores dos pontos críticos achados na Etapa 2 em f”(x). Com efeito, veja que teremos que.

Assim, segue do teste da derivada segunda que o ponto crítico q = 0 é um ponto de mínimo pois o resultado da derivada segunda nesse ponto é positivo e q = -4 é o ponto de máximo pois a derivada segunda nesse ponto resulta num valor negativo.
Por fim, podemos estudar a concavidade. Com efeito, dizemos que a concavidade é para cima se f”(x) >0 ou seja se 6x+12 > 0 que nos dá que x > -2 e f(x) será côncava para baixo se f”(x) < 0 ou seja se x < -2. Então, veja que f(x) é côncava para cima se x > -2 e para baixo se x < -2. Por fim, veja que f”(x) = 0 nos dá o ponto x = -2 que é o ponto chamado de ponto de sela da função.
Etapa 4. Sua vez Gurunauta
Então Gurunauta, aqui você já deve ser capaz de realizar o esboço do gráfico tendo em vista essas informações que nós obtemos. Para te ajudar, vamos deixar a resposta do que esperamos que você obtenha que é o seguinte gráfico.
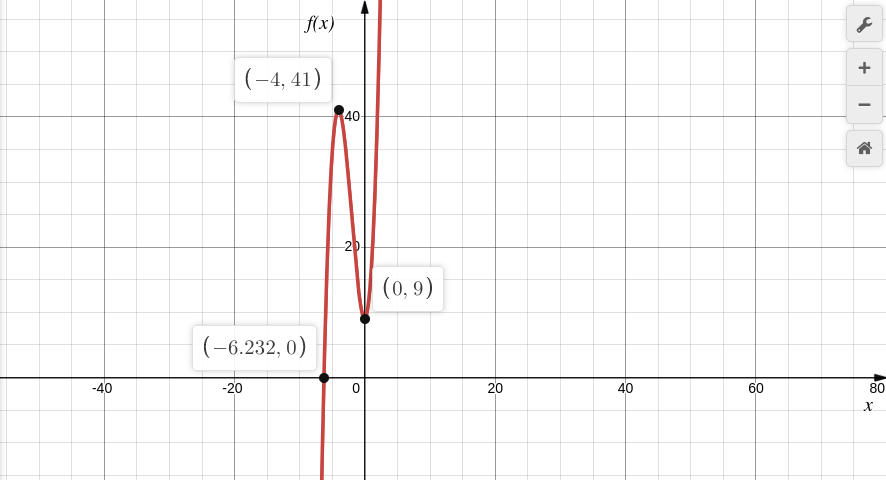
Certamente, usamos aqui um software para elaborarmos o melhor para você, todavia, se você conseguiu rascunhar algo similar já é de muito valor.
Extra especial.
Por fim, caso você ainda tenha alguma questão desse assunto pode ainda recorrer a uma fonte ilimitada de conhecimento que é a MeuGuru. Com toda certeza, há vários tutores que poderão te ajudar e muito na obtenção e geração de gráficos das mais variadas funções para você
Referências sobre gráficos de funções
- STEWART, James. Cálculo – Volume 1. 8ª ed. São Paulo: Cengage Learning, 2016.
- STEWART, James. Cálculo – Volume 2. 8ª ed. São Paulo: Cengage Learning, 2016.
- STEWART, James. Cálculo – Volume 3. 8ª ed. São Paulo: Cengage Learning, 2016.
- IEZZI, Gelson. Cálculo: Funções de uma Variável. 7ª ed. São Paulo: Atual Editora, 2001.
- FLEMMING, Diva Marília; GONÇALVES, Miriam Buss. Cálculo: Funções de Várias Variáveis. 5ª ed. São Paulo: Pearson Education do Brasil, 2006.
- KHAN ACADEMY. Disponível em: https://www.khanacademy.org/. Acesso em: [09/08/2023]
- WOLFRAM ALPHA. Disponível em: https://www.wolframalpha.com/. Acesso em: [09/08/2023].
- PAUL’S ONLINE MATH NOTES. Disponível em: http://tutorial.math.lamar.edu/. Acesso em: [09/08/2023].
- MIT OPENCOURSEWARE. Disponível em: https://ocw.mit.edu/index.htm. Acesso em: [09/08/2023].





