Nesse artigo vamos ver as integrais trigonométricas de uma forma simples, em particular as expressões recursivas. Nosso objetivo vai ser apresentar algumas integrais elementares e algumas relações importantes que vão te ajudar a calcular as integrais de recursão de funções como seno, cosseno e tangente. Então, cola comigo gurunauta e vamos juntos entender esse assunto.
Integrais trigonométricas elementares
Antes de tudo, é importante entendermos sobre o que é nosso problema. Decerto, o cálculo de integrais de funções trigonométricas é essencial para um curso de cálculo. Nesse sentido é importante conhecermos, desde as mais básicas integrais trigonométricas até algumas mais avançadas. Tendo isso em vista, vamos apresentar, agora, algumas dessaas
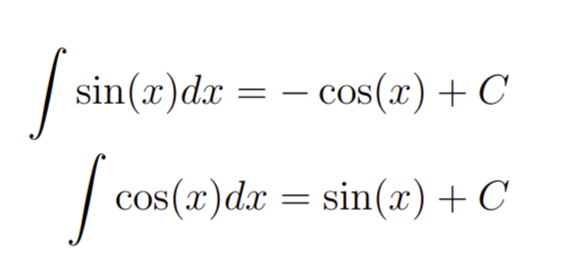
Essas duas integrais, são o ponto de partida no nosso estudo. Em verdade, elas são aquele tipo de coisa que você deve ter sempre em mente e, jamais, deve esquecer. A constante C acima vêm do fato das integrais serem indefinidas, caso fossem definidas basta prosseguirmos usando o Teorema Fundamental do Cálculo.
Nesse artigo, vamos nós importar, principalmente com as associadas as funções seno e cosseno. Em geral, você logo verá que o método usado para calcularmos as integrais que estamos interessados é o mesmo para qualquer uma das funções trigonométricas. Assim, você vai poder ver dois bons exemplos e terá a bagagem necessária para desenvolver seus próprios cálculos daqui em diante.
Integrais trigonométricas por fórmulas de recursão
Antes de irmos diretamente a como resolver esse tipo de integral, vamos apresentar a estrutura geral dele. Nesse sentido, a fórmula abaixo captura a essência da nossa discussão

onde f(x) é uma função trigonométrica, em verdade f(x) pode ser bem expressa por

e, o número n que é o expoente de f(x) é um número inteiro tal que n é maior ou igual a 2. Dito isso, nossa integral parece ser um problema suficientemente difícil de resolver, no entanto, com as técnicas corretas isso torna-se simples.
O objetivo dessas integrais é resolvê-las de forma recursiva. Em geral, vamos aplicar o processo de integração por partes o qual nos permitirá abaixar a ordem do expoente n até obtermos as integrais elementares que citamos na seção anterior. Nesse sentido, vamos ver agora dois exemplos resolvidos para que você saiba como resolver esse tipo de integral.
Integral recursiva para função seno
Nosso problema será resolver a seguinte integral

Vamos avaliar essa integral, passo a passo, a seguir

Integral recursiva para função cosseno
Nosso problema será resolver a seguinte integral

Vamos avaliar essa integral, passo a passo, a seguir

Agora, resolver as outras integrais e obter suas fórmulas de recorrência são simples. Então, deixo para que você faça as demais e consiga garantir seu aprendizado. E lembre-se para esse e quaisquer perrengues conte sempre com a MeuGuru.





