Nesse artigo, vamos falar sobre as integrais trigonométricas inversas. Fala gurunauta, com toda certeza se você passou por cálculo integral deve ter visto as famosas integrais trigonométricas inversas. Além disso, é bem capaz que essas integrais tenham tirado seu sono. Por outro lado, se você não cursou ainda essa cadeira na faculdade é bom se preparar por que esse tipo de integral realmente pode te causar problemas.
Entretanto, nós da MeuGuru queremos ajudar você dos famosos perrengues universitários. Então, vem comigo que hoje vou te ensinar uma dica de ouro para resolver esse tipo de integral e garantir aquele notão na sua prova.
O que são integrais trigonométricas inversas
Quando nos referimos as integrais trigonométricas inversas, estamos nos referindo a um tipo específico de integrando. Em particular, integrandos associados as funções trigonométricas inversas, particularmente, as funções arcsin(x), arccos(x) e arctan(x) que são associados aos respectivos integrandos.
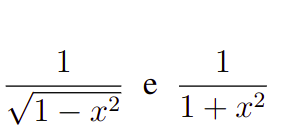
Nesse sentido, a forma geral para resolver esss integrais é usando alguma substituição. Todavia, essa mudança de variáveis ocorre de forma diferente ao que é feito nas primeiras mudanças de variáveis que estudamos em integrais. Aqui, faremos diretamente sobre nosso x.
Em particular, o grande problema dessas integrais é exatamente saber qual mudança deve ser feita. Nesse sentido, vamos agora apresentar uma dica valiosa para isso que vai te ajudar e muito a resolver esses problemas.
Uma dica de ouro
Podemos contornar o problema da mudaça de variável apresentada anteriormente com uma dica de ouro para essas funções. De fato, aqui você precisará saber muito pouco e terá em mãos uma ferramenta poderosa para saber identificar a mudança certeira que reduzirá seus problemas a simples integrandos. Então, vamos começar a construir a ideia partindo da relação fundamenta da trigonometria, com efeito.

ademais, dividindo a expressão acima por cos2(x) teremos

Com isso em mãos teremos o guia para pensarmos em como fazer a substiuição desejada. Para facilitar a vida e o entendimento, vamos aplicar a ideia no integrando 1/1+x2, então, veja o esquema abaixo.

Agora, você deverá pensar em que relação você possui uma estrutura similar a essa, isto é, o número 1 somado com uma função. Decerto, você verá que isso ocorre no caso da relação trigonométrica quando dividida por cosseno ao quadrado. Então, isso indica que a mudança a ser feita deve ser x = tan(x).
Em verdade, podemos esquematizar e sintetizar essas ideias numa tabela, com efeito.

Assim, você não precisa memorizar longas mudanças, em verdade, basta que você se lembre das relações fundamentais da trigonometria.





