Nesse artigo, vamos falar sobre o movimento harmônico simples. De fato, esse assunto é um dos tópicos pertinentes em Física 2. Não apenas isso, mas o movimento harmônico simples, ou simplesmente, MHS é um dos paradigmas que baseia grande parte dos desenvolvimentos físicos.
Logo, entender o MHS é algo primordial na física e, obviamente, necessário para você garantir a aprovação nas cadeiras de Física do seu curso. Então, vem comigo que hoje você vai entender o que é o MHS.
Oscilações harmônicas
Nesse sentido, vamos começar a entender o que é o MHS. Em suma, esse movimento é caracterizado pelas chamadas oscilações harmônicas. As quais são um tipo específico de oscilações, e possuem as seguintes características
- A dinâmica da partícula é periódica,
- O movimento ocorre em torno de uma posição chamada de posição de equilíbrio,
- Os desvios considerados são apenas lineares, ou seja, proporcionais a posição da partícula,
- O período (tempo para que uma oscilação ocorra) é constante.
Sob essas hipóteses, é possível estabelecer as oscilações harmônicas. Logo, todo corpo que esteja num movimento sob as condições acima estará num MHS.
A equação para movimento harmônico simples
Tendo em vista que, agora, conhecemos o que é o MHS. É interessante descrevermos, como esses sistemas podem ser modelados matematicamente. Para isso, vamos imaginar o modelo clássico de um oscilador harmônico, isto é, um bloco preso a uma mola que satisfaz a lei de Hooke conforme a Figura 1.
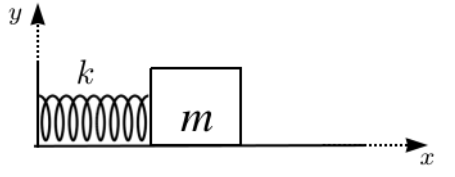
De fato, o bloquinho acima quando puxado inicia um movimento periódico de vai e vem sobre o eixo x. Não apenas isso, mas esse movimento ocorre em torno de uma posição central, a qual chamamos de posição de equilíbrio.
Ademais, é possível aplicara a segunda lei de Newton com a lei de Hooke na Figura 1, de modo a obtermos a seguinte expressão

Em geral, essa equação é uma equação diferencial de segunda ordem. Em geral, no curso de física 2 você não terá que resolver esse tipo de equação, porém, caso seja necessário você pode conferir esse artigo ou esse que lá te ensino a entender e resolver esse tipo de EDO.
Solução do MHS
No mais, de qualquer maneira, é importante que você conheça a solução do MHS. Isto é, que você saiba qual a a expressão geral de movimento para um sistema em MHS, essa é dada por

Onde, A, omega e fi são constantes e denotam:
- A é a amplitude do movimento. No caso do OH da Figura 1, é a máxima elongação da mola,
- Omega é a frequência angular do movimento,
- fi é o ângulo do deslocamento de fase. Ele aparece, apenas, quando a posição inicial do movimento é diferente de zero.
Tendo isso em vista, saiba que a maior parte das questões de física 2 irá cobrar de você o conhecimento de modelar a expressão 2 para o caso particular que ela te apresente. Ou seja, seu trabalho será identificar essas constantes e obter a expressão específica para seu MHS.
Além disso, se conhecermos a posição inicial x0 e a velocidade inicial v0 é possível escrever, a posição, velocidade e aceleração em termos desses parâmetros com efeito isso resulta no seguinte
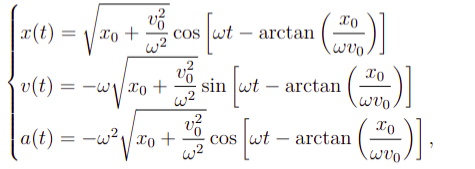
Note ainda que há uma relação entre x(t) e a(t), a qual é

que é uma relação que vale para todo corpo em MHS.
Sistemas físicos em movimento harmônico simples
Há diversos sistemas físicos que desempenham oscilações harmônicas. Em particular, podemos citar os seguintes
- Um bloco preso numa mola (sistema massa-mola),
- Um pêndulo simples (massa presa a um fio que oscila no plano),
- Um bloco de gelo parcialmente submerso em água que é pressionado para baixo,
- Um pêndulo físico (distribuição de massa que oscilação por um eixo de rotação fixo).
Além disso, há várias generalizações dos osciladores harmônicos, os quais associam-se a diversos problemas físicos relevantes como a oscilação de andares de prédios em terremotos, buracos negros e moléculas diatômicas.
E lembre-se gurunauta, sempre conte com a MeuGuru para te ajudar nos problemas acadêmicos.





