O que é uma transformação linear ? . Certamente, todos que já passaram pela cadeira de álgebra linear se depararam com uma transformação linear. Decerto, esse assunto é um dos pontos altos da cadeira de álgebra linear. Nesse sentido, se você tá pensando em correr das provas finais e garantir a aprovação no semestre, vem comigo que vou te contar exatamente o que você precisa saber sobre as transformações lineares.
A ideia por trás de uma transformação linear
A ideia que rege as transformações lineares é similar a ideia por trás das funções. Todavia, há algumas considerações e particulares que devem ser postas para essas transformações.
Primeiramente, veja que essas transformações lineares surgirão no contexto da álgebra linear. Portanto, diferentemente das funções usuais que estamos acostumados, as transformações lineares associarão vetores de um espaço vetorial a outro espaço vetorial. Nesse sentido, podemos escrever uma forma abstrata para essas transformações da seguinte maneira
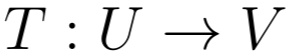
onde T representa nossa transformação, U e V são dois espaços vetoriais. Assim, a associação dos elementos de u e v pode ser exemplificada da seguinte forma

ou seja, o vetor u é aplicado em T, assim, gerando o vetor v. Quando o espaço U é igual ao espaço V dizemos que T é um operador.
A linearidade
No entanto, apenas associar vetores a outros não caracteriza uma transformação linear. Em verdade, é necessário que a transformação T satisfaça algumas propriedades que veremos agora.
Em particular, dizemos que a transformação T é linear em relação a soma se T satisfaz
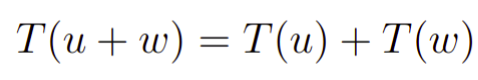
para todo u,w pertencentes ao espaço vetorial U.
e dizemos que T é linear em relação ao produto por escalar se T satisfaz
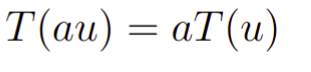
para todo escalar “a”. Quando as propriedades 1 e 2 são satisfeitas simultaneamente dizemos que T é uma transformação linear. Além de que, podemos combinar as duas propriedades em uma única só forma, com efeito
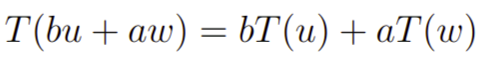
que vale para todo u, w em U e para todos os escalares b e a. Assim, fica fácil ver o que é uma transformação linear. E se você tá achando meio abstrato ainda, calma gurunauta, vem comigo que vou resolver um exercício com você passo a passo para você aprender de vez esse assunto.
Exemplo de uma transformação linear
Nesse exemplo, vamos mostrar que a seguinte transformação do espaço R2 em R2
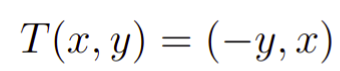
é linear. Com efeito, basta verificarmos se as propriedades 1 e 2 são satisfeitas para T. Para isso, tomamos dois vetores (x1,y1) e (x2,y2) e um escalar “a”, com isso temos que
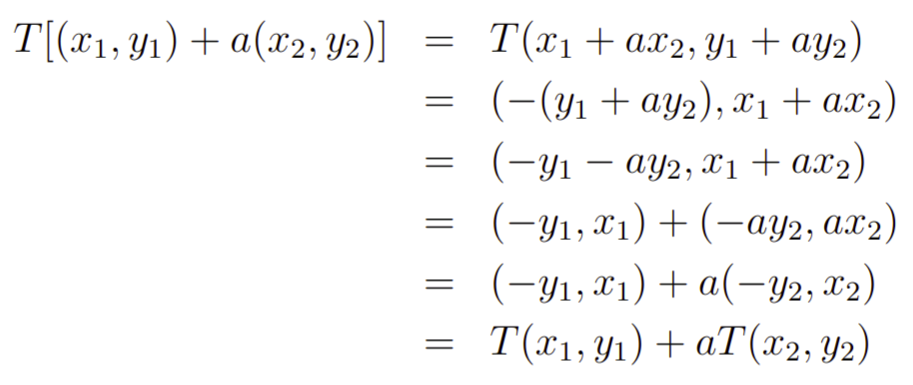
Com isso, mostramos que a transformação, de fato, é linear tanto na soma como no produto. E sim gurunauta, basta você introduzir o escalar em único vetor que isso já garantirá a linearidade da propriedade 2.
Aplicações das transformações lineares
De fato, esse assunto é muito rico, assim, tendo inúmeras aplicações. Em particular, a área das equações diferenciais se vale de todo formalismo das transformações lineares para estabelecer suas bases e fundamentações matemáticas. Tudo isso, por que tanto a derivada quando a integral são operadores lineares, de fato:

onde esses operadores estão definidos em espaços de funções diferenciáveis e integráveis respectivamente. Além disso, há um grande estudo sobre um tipo particular de transformação linear associado as integrais: as transformadas integrais.
E lembre-se gurunauta, sempre conte com a MeuGuru que vamos te ajudar.





