Fala gurunauta, nesse artigo vamos falar sobre as oscilações amortecidas no MHS. Decerto, as oscilações são um tema muito importante dentro da Física 2. De fato, já desenvolvemos um pouco sobre o MHS e sobre as oscilações forçadas.Tendo isso em vista, vamos agora nos adentrar nas oscilações amortecidas, as quais constituem um tipo importante de oscilações na física.
O que são as oscilações amortecidas
Em suma, as oscilações amortecidas são um tipo específico de oscilações, as quais ocorrem quando há a presença de um agente dissipativo no sistema. Esse agente haje com intuito de dificultar o movimento, por exemplo, o atrito das superfícies, ou mesmo a viscosidade do meio.
Nesse sentido, podemos partir da segunda lei de Newton e escrever uma expressão para esse tipo de movimento. Para isso, consideraremos um tipo de dissipação originado por uma força F = -cx’, isto é, proporcional a velocidade do corpo. Então, com isso teremos a seguinte variação do MHS:

Dividindo tudo por m teremos que
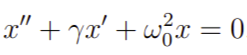
onde, gamma é o parâmetro que denota a intensidade do amortecimento e omega0 é a frequência de oscilação natural assim como o visto nas oscilações forçadas.
Oscilações amortecidas: equação de movimento
Agora, veja que a determinação da posição x(t) para a Expressão 2 fica a depender dos valores das contantes gamma e omega0. Em particular, usando o método visto para equações diferenciais de segunda ordem podemos obter o seguinte

onde lambda é o valor característico para as soluções do tipo eλt que estamos procurando. Assim, usando o método de bhaskara obtemos que as soluções para lambda são tais que

Em suma, nesse caso não podemos obter uma expressão fechada para as oscilações amortecidas. Em verdade, aqui ficamos a depender dos valores de gamma e omega0. No entanto, podemos analisar alguns casos possíveis para os valores de lambda e assim termos três soluções possíveis para esse tipo de solução, as quais são os amortecimentos subcrítico, supercrítico e crítico.
Amortecimento subcrítico
Nesse caso, temos um amortecimento que ocorre ainda com a presença do movimento periódico. Em suma ele acontece quando temos a seguinte condição

Nesse caso, a solução do sistema amortecido fica dada por

Note que o perfil do movimento oscilatório é mantido pelas funções seno e cosseno. Por outro lado, a exponencial negativa age de modo a fazer com essa oscilação decaia e termine. De fato, o gráfico para essa solução pode ser visto na Figura 1.

As curvas psi de vermelho tracejado são chamadas de envoltórias do movimento.
Amortecimento supercrítico
Por outro lado, quando temos a seguinte condição

o amortecimento é dito supercrítico. Aqui a solução da equação de movimento é a seguinte

cujo gráfico perde o caráter oscilatório e o sistema tende apenas a diminuir de forma suave, conforme Figura 2.

Amortecimento crítico
Por fim, quando temos a condição

Nesse caso, o movimento crítico perde o total comportamento oscilatório. Além disso, o sistema tende rapidamente a parar sua dinâmica. De fato suas soluções são:

Expressão 10. Solução para o amortecimento crítico.
O gráfico correspondente se assemelha ao amortecimento subcrítico, todavia, a curva cai mais rapidamente para zero, veja a Figura 2.

Agora já sabe gurunauta, para quaisquer problemas universitários vem com a MeuGuru que vamos te ajudar.





