Fala gurunauta, hoje vamos falar sobre oscilações harmônicas num fluido. Na verdade, esse artigo pode ser visto como um anexo a outros textos aqui do Blog da MeuGuru, em particular, esse aqui ou esse. De fato, tanto as oscilações harmônicas quanto os fluidos são sistemas físicos muito importantes. Tendo isso em vista, nesse artigo vamos resolver um problema, passo a passo, que relaciona esses dois assuntos. Pois assim, você gurunauta verá exatamente como relacionar diferentes assuntos, por conseguinte, melhorando seu repertório e suas habilidades em Física.
Apresentando e entendendo o problema
O problema que iremos solucionar será o seguinte. Consideraremos um vaso comunicante conforme mostrado na Figura 1.

Além disso, consideraremos também que há um fluido de densidade ro, que a secção transversal do vaso comunicante tem área A e que l seja o comprimento total da coluna do tubo.
De posse disso, e assumindo que o eixo vertical corresponde a componente z, vamos mostrar que, o fluido dentro do tubo em U executa uma oscilação harmônica.
Solução passo a passo e as oscilações harmônicas
Tendo em vista que o problema já foi apresentado, agora vamos, buscar resolver essa questão passo a passo. Primeiro de tudo, devemos entender que o fato do tubo ser em U é significativamente importante pois forma um vaso comunicante. Esses vasos são de extrema importância para hidráulica, além de que isso permite que pressão em todo o fluido seja a mesma.
Em particular, a um importante resultado dos vasos comunicantes que usaremos nessa solução: a variação da altura do líquido das colunas é igual.
De posse disso, primeiramente, vamos obter a energia potencial do sistema. Com efeito, sabemos que o fluido tem uma determinada massa M, logo está sujeito a ação da força gravitacional. Além disso, podemos associar então a uma porção do fluido uma energia potencial gravitacional, associado ao desnível dos vasos, conforme figura 3.
Então, onde a altura h será exatamente a medida z do deslocamento do fluido e logo, podemos obter a seguinte expressão para a energia potencial gravitacional.
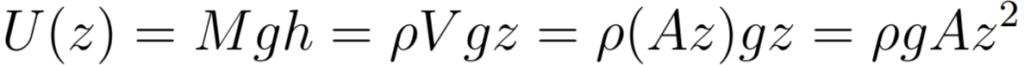
Ademais, como estamos assumindo que a única força atuante é a força gravitacional, podemos, então já empregar a segunda lei de Newton do seguinte modo:
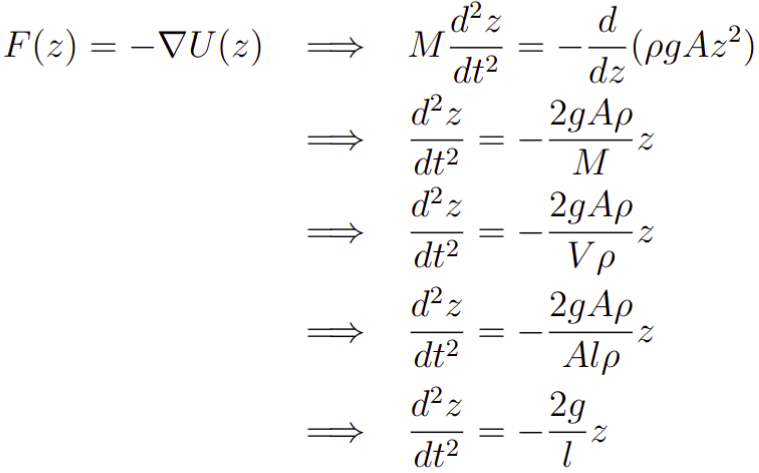
Onde, usamos que a massa M do fluido é exatamente igual ao seu volume vezes sua densidade. Além disso, como o fluido é homogêneo sabemos que sua densidade é igual para qualquer parte que pegarmos dele, ou seja, rho = A l, onde l seria a altura total do fluido se estivesse num único tubo.
Então, agora, note que se definirmos a seguinte frequência:

veremos que a Equação anterior se reduz a um oscilador harmônico. Assim, o problema fica resolvido.





