
O paradoxo de Zenão é uma intrigante ideia que associa questões filosóficas e fisico-matemáticos sobre a descrição do movimento de corpos. Decerto, essas questões foram propostas por um filósofo grego chamado Zenão. Em suma, seus paradoxos desafiam completamente nossas perpecepções empíricas sobre as leis dos movimentos, nos levando a questionar se realmente seria possível realizarmos alguma ultrapassagem.
De fato, os paradoxos de Zenão são ideias incríveis que permitem que nós consigamos refletir sobre questões conceituais importantes, em particular a ideia de referenciais. Ademais, as ideias propostas por Zenão ainda são enriquecedoras para você gurunauta que entrou em um curso de exatas. Pois, elas podem fazer com que você comece a enchegar aquelas aulas de dinâmica e cinemática de formas bem diferente.
Nesse sentido, nesse artigo nós vamos te apresentar, de forma simples e fácil os importantes paradoxos de Zenão. Então gurunauta, vem comigo que hoje nós vamos nos enveredar sobre o mundo da filosofia, ciência, matemática e claro, dos paradoxos.
As ideias gerais sobre o paradoxo de Zenão
De início, é importante entendermos que não temos apenas um paradoxo. De fato, quanto nos referimos a essa ideia estamos mencionando um conjunto de paradoxos que juntos constituem as bases das ideias que Zenão buscava expresssão.
Nesse sentido, destacamos que os dois casos principais desse problema são: a corrida entre aquiles e a tartaruga e o problema de flecha ao alvo. Tendo isso em vista, vamos detalhar cada uma dessas duas consagradas ideias a seguir.
O paradoxo de aquiles e a tartaruga
De início, vamos começar com o paradoxo de Aquiles e a tartaruga. Com efeito, esse é um dos paradoxos mais famosos de Zenão de Eleia. Em suma, a ideia básica do paradoxo consiste em analisarmos uma corrida entre uma tartaruga e o heroi grego Aquiles.
Nesse sentido, imagine que a tartaruga já está na frente de Aquiles. Agora, você deve estar sendo levado a ver que nosso herói grego logo passará a tartaruga uma vez que com certeza ele é bem mais rápido do que ela. Entretanto, Zenão de Eleia vai descordar de você e dizer que isso nunca acontecerá.
De fato, a argumentação do filósofo é de que sempre que Aquiles alcançar a posição da tartaruga anterior, a tartaruga já terá avançado um pouco. E, uma vez que a tartaruga sempre avança um pouco, Aquiles nunca conseguirá alcançá-la. Portanto, o paradoxo argumenta que, mesmo que a diferença entre Aquiles e a tartaruga seja infinitesimal, Aquiles nunca será capaz de ultrapassá-la. Então, nossa tartaruga se consagrará como campeã de uma corrida contra um herói grego.
Essa ideia pode parecer absurda, mas será que você gurunauta consegue entender a problemática dessa questão ?. Bom, o entendimento desse problema não é trivial e com intuito de estudarmo e entendermos até mesmo melhor o mesmo vamos ao próximo paradoxo de Zenão.
O paradoxo de Zenão: A flecha em movimento
Agora, vamos conhecer o paradoxo da flecha é um dos paradoxos de Zenão de Eleia. Neste paradoxo, Zenão questiona a possibilidade de que um objeto possa se mover de um ponto a outro, argumentando que o movimento é uma ilusão.
Bom, em suma esse paradoxo é descrito da seguinte maneira. Com efeito, pense numa flecha em movimento até um alvo. Agora, de acordo com a argumentação de Zenão há um momento específico, em que a flecha deve estar em repouso, pois se ela está ocupando um ponto no espaço, então ela não pode estar se movendo para esse ponto. Além disso, a flecha só pode estar em um lugar de cada vez, então em qualquer momento, ela não está se movendo para onde está atualmente, mas também não está se movendo para onde não está.

De fato, essa dicussão nos leva a questionar se é possível nos movermos no espaço. Em verdade, essa é uma questão delicada que nos leva a ver a necessidade de entendermos conceitualmente aspectos da nossa realidade física objetiva. Com efeito, Zenão argumenta que o movimento é algo ilusório e feito apenas de momentos fixos e estáticos no tempo e no espaço.
A solução de Zenão
Então, agora que já te apresentamos os incríveis paradoxos de Zenão, está na hora de pormos um fim aos nós e enlaces mentais dos mesmos. De fato, agora vamos entender como esses paradoxos são resolvidas. Em verdade, os parodoxos de Zenão são solúveis e podem ser entendidos por nós.
Nesse sentido, é importante citarmos que o próprio Zenão com seus paradoxos quis mudar a percepção e o entendimento da ideia de movimento com a composição de instantâneos. Ademais, ele ainda propós a ideia de que o espaço é composto de uma infinidade de pontos e que é impossível percorrê-los todos em uma quantidade finita de tempo. Ele argumentava que, se considerarmos o espaço como um conjunto de pontos, então qualquer movimento de um ponto a outro exigiria que se percorressem uma quantidade infinita de pontos, o que seria impossível.
Entretanto, esses argumentos de Zenão, por mais que sejam interessantes, podem hoje já serem explicados de forma objetiva através de teorias científicas. Nesse sentido, agora vamos ver algumas dessas teorias.
O Cálculo e as leis da Mecânica contra os paradoxos de Zenão
Com efeito, talvez a primeira grande queda das ideias propostas por Zenão foram advindas do Cálculo infinitesimal e das leis da Mecânica. De fato, o cálculo nos fornece ferramentas analíticas poderosas que mostram que os infinitos instantâneos de Zenão resultam em algo finito. Com efeito, vamos esquematizar essa questão com a Figura a seguir.
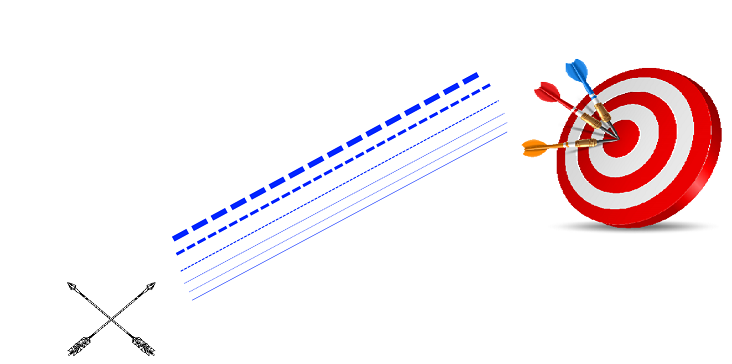
Aqui, as linhas tracejadas mostram a trajetória percorrida pela flecha discretizada nos instantâneos de Zenão. Entretanto, quando comecamos a pensar na própria ideia do filósofo e criamos mais e mais instantâneos, em verdade, tanto quanto possamos começamos a ter uma situação em que a discretização da trajetória se põem de forma contínua. Decerto, isso é retratado, pelas linhas pontilhadas acima que vão sendo cada vez mais particionadas.
Assim, temos uma situação que pode ser explorada pelas ferramentas do cálculo. Com efeito, o problema aqui é a nossa contraintuição com a infinitude. De fato, podemos pensar que ao somarmos infinitos números devemos encontrar algo infinito. Todavia, a teoria do cálculo, em particular das séries nos mostra que é possível que esse resultado seja um número finito e é exatamente isso que ocorre no caso dos instantâneos de Zenão.
Como as progressões geométricas aparecem no paradoxo de Zenão
Outro ponto interessante nesse sentido é acerca do paradoxo do movimento de aquiles e a tartaruga. Com efeito, podemos reestruturar esse problema para a seguinte forma. Pensamos que, ao invés de olharmos para o movimento de Aquiles pensamos em analisar a cinemática da tartaruga.
Com efeito, note que como a tartaruga está sempre a andar, ela sempre irá chegar a uma distância a frente. Então, vamos tomar a distância que levou metade do tempo T da distância anterior e assim sucessivamente. De fato, podemos enumerar os pontos si do movimento e então teremos que para cada movimento da tarturga terar-se o seguinte:
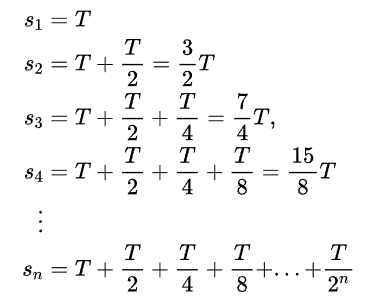
De início, é possível que você pense que essa soma será infinita como imaginaríamos de acordo com Zenão. Entretanto, o resultado mostrará que se n ficar tão grande quando queiramos é possível mostrarmos que a tartaruga levará um tempo de 2 T para essa trajetória completa.
De fato, isso ocorre por que temos aqui uma progressão geométrica cujo razão é menor que 1. Incrível em gurunauta, um problema filosófico pode ser resolvido com matemática elementar que você viu enquanto estudava funções durante a escola.
Referências
- Artigo: HUGLY, Peter S.; SAYWARD, Charles. Zeno’s Paradoxes. In: The Stanford Encyclopedia of Philosophy. Winter 2018 Edition. Disponível em: https://plato.stanford.edu/archives/win2018/entries/zeno-paradoxes/. Acesso em: 07 maio 2023.
- Livro: RUSSELL, Bertrand. A História da Filosofia Ocidental. Rio de Janeiro: Ediouro, 2012.
- Artigo: GARCIADIEGO, Javier. Zeno’s Paradoxes. In: The Internet Encyclopedia of Philosophy. Disponível em: https://iep.utm.edu/zeno-par/. Acesso em: 07 maio 2023.





