Saber regra de três simples é algo essencial para você ir bem em matemática e crescer cada vez mais nessa área. Com efeito, grande parte dos problemas associados a matemática básica podem, por vezes, serem reduzidos ao emprego de regras de três simples em virtude do uso de proporções e/ou razões conhecidas entre as grandezas envolvidas no problema. Ou seja, compreender bem regras de três te permitirá ter uma melhor visão de assuntos elementares da matemática e logo melhorando sua fundação nessa área.
Então, é nesse sentido que nós, da MeuGuru decidimos desenvolver esse texto para você querido gurunauta. Em suma, nosso objetivo aqui será apresentar um tutorial elementar sobre regras de três simples de modo que seja possível a você gurunauta que deseja entender esse assunto conhecer e saber aplicar essa técnica em algumas situações elementares.
Ademais, esse é o primeiro artigo da série matemática básica aqui no blog da MeuGuru. Com efeito, essa série conterá diversos artigos envolvendo tópicos relevantes da matemática que te ajudarão a fundamentar cada vez mais a sua base matemática. Então, vem com a gente nesse primeiro artigo dessa série que hoje vamos começar a desmistificar as problemáticas da matemática a partir de sua base.
Entendendo o que é uma regra de três
Antes de tudo começaremos nossos esforços em entender o que é uma regra de três. Com efeito, as regras de três surgem a partir de igualdades matemáticas que, em geral, são conduzidas a partir de equivalências ou proporções bem estabelecidas por alguma regra, conhecimento ou mesmo uma lei natural. Nesse sentido, a geometria é um dos campos que mais toma destaque quando falamos desse assunto, uma vez que, diversas proporções podem ser obtidas a partir de relações métricas e/ou trigonométricas entre figuras.
Além disso, não só apenas com figuras planas mas há ainda relações que podem ser estabelecidas com grandezas de volume. Em particular, é possível estabelecer, sob domínio da geometria plana condições que fazem com que haja razões bem estabelecidas e constantes entre lados e volumes de certas figuras, a citar, temos a pirâmide que evidencia sua relação de proporcionalidade do lado e seu volume.
A ideia de proporção em regras de três
Assim, o que podemos desde já afirmar sobre esse assunto é que o mesmo ocorre e surge de relações de proporcionalidades. Portanto, além do que citamos de aplicações em geometria plana e afins há sem dúvidas diversas outras aplicações como na química em cálculo estequiométrico, em problemas de matemáticos envolvendo matemática financeira e diversos outros aspectos que fazem urgir as regras de três.
Esquematicamente, podemos dizer que a regra de três emerge de uma conexão entre uma quantidade a e uma quantidade b onde dizemos que “a” está para “b” se “a” é proporcional a “b”, ou seja, se “a” cresce então “b” cresce ou se “a” diminui então “b” diminui. Na figura a seguir esquematizamos isso.
Todavia, a depender da quantidade de termos e grandezas envolvidas podemos ter diferentes regras que permitirão computar corretamente essas quantidades. Nesse sentido, há dois exemplos bem interessantes que devemos considerar que são as regras de três simples e compostas.
A Regra de três simples
Com efeito, chegamos então a parte de grande interesse do nosso artigo. Decerto, nosso intuito aqui é te mostrar o que é uma regra de três simples e como você pode computar grandezas envolvidas a partir dela. Em geral, essa é a regra que você mais irá se deparar ao longo dos seus estudos uma vez que ela é mais frequente em problemas cotidianos e ainda por ser incrivelmente relevante em diversos cenários de aplicações, inclusive, a título de vestibulares a mesma é extensivamente cobrada em provas e avaliações.
Em suma, a regra de três simples aparece como uma forma de resolver problemas onde temos duas grandezas físicas que admitem certa proporção. Particularmente, o ponto alvo aqui é entender que são duas e apenas duas grandezas físicas por exemplo, volume e altura, quantidade de ovos para quantidade de bolo, quantidade de leite para pão, quantidade de funcionários para uma determinada tarefa dentre outros exemplos.
Assim, a relação de regra de três simples é estabelecida de modo que alguma proporção seja conservada e com isso garanta que o problema se mantenha nas mesmas condições iniciais. Então, o caso mais geral que podemos citar é quando temo duas quantidades a e b que ficam em proporção com c e d de modo a termos a seguinte expressão matemática
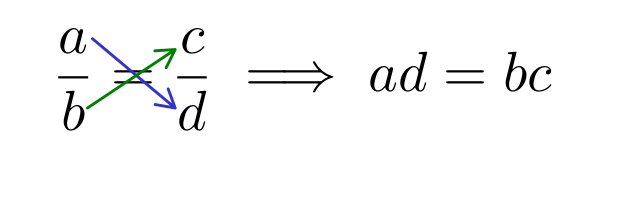
as setas acima indicam o sentido que ocorre a operação de multiplicação. Logo, em geral você tem que para cada termo acima o conhecimento de dois, que são aqueles que estabelecerão a proporcionalidade, ademais, você terá ainda o conhecimento de outro termo que será aquele que dado você o ter e sabendo da proporção você poderá determinar o último. Com intuito de mostrar e evidenciar essa passagem apresentaremos um exemplo prático no fim do artigo.
A Regra de três composta: Um breve comentário !
A regra de três composta, também conhecida como regra de três composta inversa ou regra de três composta mista, é um método matemático utilizado para resolver problemas envolvendo grandezas proporcionais e inversamente proporcionais. É uma extensão da regra de três simples, que lida com duas grandezas proporcionais. Não entraremos em detalhes nesse artigo mas logo logo teremos um texto específico sobre ela.
Exemplo prático de regras de três simples
Agora, vamos esclarecer um pouco mais a regra de três simples. Com efeito, vamos ao problema de determinar a altura h de um lado de um triângulo sabendo que esse triângulo está dentro de um triângulo de altura H e lado S. Bom, essa situação está esquematizada a seguir e você pode ver ela claramente.

Bom, faremos essa questão de duas formas que evidenciarão o uso de regra de três. Certamente, os mandamentos da geometria plana euclidiana nos dizem que para essa situação há naturalmente uma proporção entre alturas dos triângulos e o lado de suas bases. Mais precisamente, a geometria euclidiana nos diz que h está para H como p está para S e isso pode ser posto matematicamente como
- h / H = p / S => hS = pH => h = pH/S.
e logo a altura h fica determinada com o uso da regra de três onde simplesmente usamos o que havíamos mencionado anteriormente. Todavia, podemos ainda obter essa relação via trigonometria simples apenas analisando que o ângulo theta é associado a essas duas quantidades via tangente com efeito veja que
- tg(theta) = h/p e tg (theta) = H/S = > h/p = H/S => H/h = S/p
e temos a mesma relação vinda da proporcionalidade da regra de três simples.
Referências
- IEZZI, Gelson; DOLCE, Osvaldo; DEGENSZAJN, David; PÉRIGO, Roberto. Fundamentos da Matemática Elementar: Volume Único. São Paulo: Atual, 2019.
- GIOVANNI, José Ruy; CASTRUCCI, Benedito; GIOVANNI JR., José Ruy. A Conquista da Matemática: Volume Único. São Paulo: FTD, 2018.
- DANTE, Luiz Roberto. Matemática Contexto & Aplicações: Volume Único. São Paulo: Ática, 2019.
- GOMES, José Ruy; MACHADO, Antônio dos Santos; LOPES, José Lellis. Matemática: Paiva para o Ensino Médio. São Paulo: Moderna, 2019.
- BONJORNO, José Roberto; GIOVANNI, José Ruy. Matemática Fundamental: Uma Nova Abordagem. São Paulo: FTD, 2018.
- SILVA, Andréa Aparecida Ferreira da. A importância do ensino da Matemática no ensino fundamental e médio. Revista Brasileira de Educação Matemática, São Paulo, v. 22, n. 42, p. 131-143, maio/ago. 2017.
- Brasil Escola. Regra de Três Composta. Disponível em: https://brasilescola.uol.com.br/matematica/regra-tres-composta.htm. Acesso em: 08 jan. 2024.
- ANTON, Howard; RORRES, Chris. Álgebra Linear com Aplicações. Porto Alegre: Bookman, 2012.
- STEINBRUCH, Alfredo; WINTERLE, Paulo. Geometria Analítica. São Paulo: Pearson, 2009.
- FLEMMING, Diva Marília; GONÇALVES, Miriam Buss. Cálculo II: Funções de Várias Variáveis. São Paulo: Pearson, 2013.





