Nesse artigo, vamos falar sobre sequências numéricas. Em particular, vamos entender o que são as sequências numéricas de números reais.
Por que estudar sequências numéricas
Primeiramente, é importante que você saiba que esse assunto é muito importante. De fato, ele recorrente em disciplinas de cálculo e em análise matemática. Nesse sentido, conhecer os fundamentos sobre sequências torna-se essencialmente relevante. Além disso, tendo em mãos o arcabouço teórico sobre sequências é possível estabelecer um critério para continuidade de funções.
Sequências numéricas: o que são
Tendo isso em vista, vamos começar entender sequências a partir de sua definição. Todavia, definir sequências é algo essencialmente simples, pois, na verdade, elas são apenas um tipo específico de funções. De posse disso, vamos a seguinte definição.
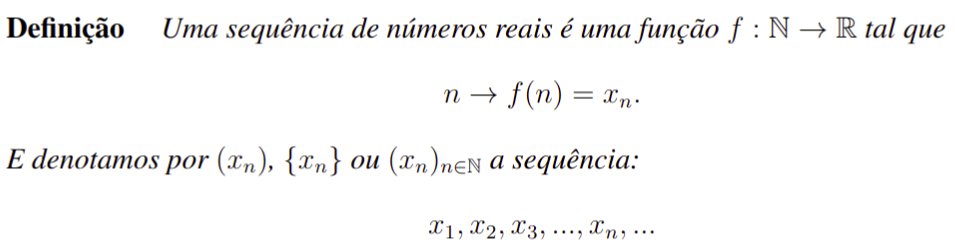
Com isso em mãos, torna-se possível entender melhor esse assunto. Em particular, podemos até mesmo já exibir alguns exemplos, com efeito.
- xn =1/n
- xn = n. Sequência identidade,
- xn=cos(nπ)
Em muitas situações, nosso interesse será entender como essas sequências se comportam para quando n torna-se suficientemente grande, mas isso exploraremos na seção seguinte.
O limite de sequências
Com efeito, vamos agora falar um pouco sobre limites. Decerto, você já deve ter visto e/ou calculado limite de funções, com isso em mente, saiba que para sequências a situação é bem mais simples. De fato, aqui você não terá a preocupação de várias possibilidades de onde o limite irá ir, em suma, no contexto de sequências sempre estaremos interessados no caso em que n tende ao infinito. Portanto, nosso objetivo sempre será avaliar o seguinte.

Ademais, sabemos que já do estudo de funções que nem sempre um limite existe. Por conseguinte, em sequências essa situação não será diferente, porém, aqui separamos isso em dois casos:
- Se o limite da Expressão 1 existe e é finito, então dizemos que a sequência xn é convergente.
- Se o limite da Expressão 1 não existe ou é infinito, então dizemos que a sequência xn é divergente..
Para o primeiro caso, é importante enunciarmos até mesmo a definição formal de uma sequência convergente. Com efeito, vamos a ela

Em suma, essa definição diz que a partir de um número n0 os termos da sequência xn tendem a ficar suficientemente próximos do número x que é o limite da sequência.
Exemplo de uma sequência
Consideremos a sequência 1/n. Então, temos que os termos gerados são

Por exemplo, para a sequência 1/n temos

Agora, veja que se plotarmos o gráfico da sequência teremos o seguinte

Com isso, o gráfico da Figura 1 realmente nos dá o indicativo visual do que a definição formal de limite convergente afirma. Os pontos vermelhos na Figura 1, tendem a aproximar-se e ainda aproximar-se de zero que é o imite da sequência estudada.
E com isso gurunauta, chegamos ao fim de mais um artigo. Lembre-se aluno, ainda tendo problemas na vida universitária? contate a MeuGuru que vamos te ajudar.





