Teoria do caos: Explicando o efeito borboleta

A teoria do caos é uma teoria que emerge da matemática aplicada que estuda sistemas altamente sensíveis as suas condições inciais. Assim, essa teoria é responsável por dedicar-se a descrição da interação de problemas complexos, imprevisíveis e aleatórios.

Por outro lado, a teoria do caos também se destaca por sua forte presença na cultura pop com diversas produções audiovisuais que empregam conceitos da teoria em seus enredos de ficção científica. Nesse sentido, destaca-se o clássico efeito borboleta que relaciona a correlação e causalidade de fenômenos distintos como o bater de asas de uma borboleta com a produção de furacões pelo mundo.

Tendo isso em vista, nesse artigo hoje nós da MeuGuru vamos te falar um pouquinho sobre essa elegante teoria da matemática. Portanto, vem comigo gurunauta que agora vamos começar a entender sobre como o caos é algo iminente em nossas vidas.

A noção determinística da natureza

Para começarmos nossa discussão, devemos remontar a um dos marcos históricos da ciência: as Leis de Newton. Com efeito, quando as leis de Newton foram propostas a comunidade científica da época começou a questionar-se muito mais sobre os aspectos filosóficos que essas leis trariam. De fato, os resultados de Newton diziam que os corpos em movimento podiam ser descritos por leis matemática, e suas trajetórias dinâmicas, em qualquer instante de tempo, deveriam satisfazer a segunda lei de Newton.

Nesse sentido, a comunidade científica, em particular impulsionada pelo matemático Laplace começou a disseminar a concepção de que a natureza seria determinística. Isto é, já que as trajetórias dos corpos podiam ser descritas matematicamente, isso significa que a forma com que os corpos se moveriam ao longo do tempo já estaria predita. Portanto, todos os movimentos, desde o andar de pessoas até a dinâmica celeste (planetas, sol, asteroides e afins) seria possível de ser determinada, ou seja, determinística.

A farsa da natureza determinística

Entretanto, essa noção determinística que advêm do sucesso das leis de Newton era na verdade falsa. Decerto, isso decorre do fato de que as leis de Newton são equações que regem apenas uma parte, substancialmente pequena, do nosso pequeno universo. Assim, a medida que os estudos sobre dinâmica celeste progrediram, os avanços da teoria da relatividade de Einstein e a mecânica quântica consolidou-se descobrimos que natureza e seus fenômenos não são determinísticos, em particular com a teoria do caos. Com efeito, o despontar dessas áreas nos revelaram que a natureza é, na verdade, aleatória e probabilística sendo, então, redida por probabilidades.

Surgimento da teoria do Caos: Os fenômenos caóticos

Seguindo o espírito das várias áreas que mostraram que a natureza não é determinística, surge ao longo do século XX a teoria do caos. Com efeito, seu despontar ocorre na entre 1960 e 1970 com os estudos meteorológicos de Edward Lorenz (Esse Lorenz não é o mesmo Lorentz da física da relatividade). Em particular, seus estudos versavam sobre o desenvolvimento de um modelo matemático simplificado para a previsão climática com uso de equações diferenciais.

Os experimentos de Lorenz

Assim, Lorenz buscava realizar experimentos computacionais que empregavam resolver, com auxílios de computadores e recursos numéricos, essas equações. Nesse sentido, em um dos seus experimentos, ele empregou dados arredondados, como por exemplo 0,506 em vez de 0,506127 com intuito de economizar recursos computacionais. Entretanto, essa simples aproximação de Lorenz o encaminhou para um novo ramo da ciência.

De fato, ao arredondar os seus parâmetros o matemático e meteorólogo obteve resultados do modelo completamente diferentes. Então, isso fez Lorenz perceber que pequenas variações nas condições iniciais poderiam levar a resultados amplamente divergentes. Ele descreveu esse fenômeno como o “efeito borboleta”, uma metáfora que ilustra a sensibilidade às condições iniciais.

Além disso, os resultados de Lorenz sobre a previsão climática levaram a obter um famoso modelo matemático que ficou conhecido como o Atrator de Lorenz. Com efeito, apresentamos esse atrator em seguida.

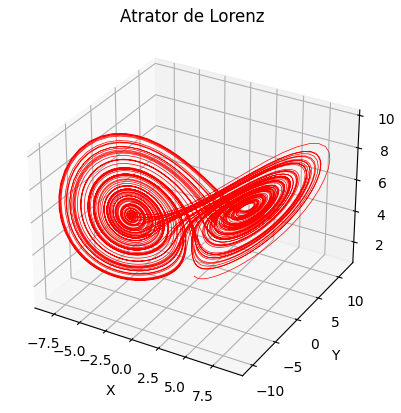
As contribuições de Mandelbrot

Após Lorenz, diversos outros pesquisadores, em particular físicos e matemáticos, se debruçaram a contribuir para a estruturação dessa teoria. Nesse sentido, e no mesmo período, temos o importante trabalho de Mandelbrot, o qual introduziu o conceito de fractais, que são formas geométricas complexas e repetitivas encontradas na natureza. Com efeito, o matemático foi capaz de mostrar que esses padrões fractais podiam ser gerados a partir de equações matemáticas simples, e que eles exibiam propriedades caóticas e autossimilares. Com intuito de ilustrar isso, tem-se o famoso conjunto de Mandelbrot que é apresentado a seguir.

A introdução de não linearidades

Ademais, devemos destacar a contribuição do matemático Stephen Smale, que estudou os chamados sistemas dinâmicos não lineares. De fato, rompendo as ideias clássicas de estudar apenas problemas lineares, isto é problemas em que as variáveis estejam sempre elevadas ao expoente 1 e/ou afins, ele foi capaz de demonstrar que mesmo sistemas matemáticos simples, quando apresentam comportamento não linear, podem exibir uma variedade de comportamentos complexos e caóticos.

O estado da arte da teoria do caos

A partir desses avanços, a teoria do caos começou a se desenvolver como um campo interdisciplinar, abrangendo matemática, física, biologia e outras disciplinas científicas. Ademais, com o avanço da computação, já na década de 1980, os pesquisadores começaram a usar computadores para simular e visualizar sistemas caóticos. Assim, permitindo uma melhor compreensão dos padrões e comportamentos complexos que surgem a partir de equações simples.

Por outro lado, diversas pesquisas nessa área ainda são conduzidas de forma teórica, principalmente sobre as perspectivas da matemática pura. Com efeito, essas pesquisas localizam-se na área de sistemas dinâmicos, em particular, o matemático brasileiro Artur Avila que foi um dos ganhadores da Medalha Fields (prêmio equivalente ao Nobel da matemática), e único brasileiro a receber a honraria, desenvolve parte de suas pesquisas nessa área.

Aplicações da teoria do caos

Assim, a teoria do caos tem ganhando forte aplicabilidade dado aos intensos estudos conduzidos na área que reveleram fenômenos caóticos em vários sistemas. Assim, ela vêm sendo fortemente aplicada em várias áreas, fornecendo insights sobre fenômenos naturais, comportamento humano, sistemas econômicos e muito mais, como os que seguem abaixo.

1. Movimento de corpos celestes: O sistema solar é um exemplo de um sistema dinâmico que exibe comportamento caótico.
2. Pêndulo duplo: Um pêndulo duplo consiste em dois pêndulos acoplados.
3. Conjunto de Mandelbrot: O conjunto de Mandelbrot é uma imagem fractal gerada a partir de uma simples equação matemática.
4. Mapa logístico: O mapa logístico é um modelo matemático simples que descreve o crescimento populacional em um ambiente limitado.
5. Ritmos cardíacos irregulares: O coração humano pode exibir ritmos cardíacos irregulares, conhecidos como arritmias.
6. Padrões de crescimento populacional: O crescimento de populações biológicas pode ser influenciado por fatores como competição, predação e disponibilidade de recursos.
7. Tomada de decisões e teoria do jogo: A teoria do caos pode ser aplicada à análise de estratégias de tomada de decisões em situações complexas, como jogos estratégicos ou negociações.
8. Dinâmica de sistemas sociais: A sociedade é composta por diversos sistemas sociais interconectados, como redes sociais, comportamento de consumo e dinâmica de opiniões.

Efeito borboleta e a teoria do caos

Agora, vamos adentrar a discussão do famoso efeito borboleta. Com efeito, esse termo é uma metáfora usada na teoria do caos para descrever a sensibilidade às condições iniciais em sistemas dinâmicos complexos. Em particular, essa metáfora foi uma forma simples de Lorenz poder explicar suas ideias sobre a importância da sensibilidade das condições iniciais dos sistemas.

Em particular, podemos enunciar, para nosso contexto brasileiro, essa ideia da seguinte forma: suponha que uma borboleta bata suas asas no Brasil e, devido à sensibilidade às condições iniciais, isso poderia desencadear uma série de efeitos que, eventualmente, resultariam em mudanças climáticas significativas em outra parte do mundo, como a formação ou não de um furacão.

Dessa forma, a metáfora associa as pequenas batidas de asas da borboleta com fenômenos climáticos catastróficos. Com isso, a ideia geral desses sistemas caóticos/complexos é exemplificada por Lorenz.

O efeito borboleta na cultura pop

De fato, a ideia simples introduzido nessa metáfora por Lorenz permitiu um entendimento simples e prático desses problemas. Em particular, isso foi um ponto chave que permitiu que as ideias de Lorenz se disseminassem para muito além do meio acadêmico. Decerto, o conceito do ”efeito borboleta” da teoria do caos se tornou bastante popular e encontrou seu caminho na cultura pop em várias formas. Aqui estão alguns exemplos notáveis:

1. Filmes e séries de televisão: Vários roteristas empregam o efeito borboleta como elemento principal no enredo defilmes e séries que exploram a noção de eventos aparentemente insignificantes que desencadeiam grandes consequências. Filmes como “Efeito Borboleta” (2004) e “Donnie Darko” (2001) exploram essa ideia em tramas complexas e misteriosas.
2. Literatura: Aqui, vemos que os autores de obras literárias buscam introduzir esse conceito, especialmente na ficção científica e nos gêneros de viagem no tempo. O livro “A Brief History of Time” de Stephen Hawking menciona o efeito borboleta e seu impacto no entendimento da física moderna.
3. Música: O termo “efeito borboleta” também foi adotado em letras de músicas e títulos de álbuns. Por exemplo, a banda norueguesa A-ha lançou um álbum em 2000 intitulado “Minor Earth Major Sky”, com uma faixa chamada “Butterfly, Butterfly (The Last Hurrah)”.

Referências

• PARKER, Barry R. Chaos: Making a New Science. University of Chicago Press, 2004.
• LORENZ, Edward N. Deterministic Nonperiodic Flow. Journal of the Atmospheric Sciences, v. 20, n. 2, p. 130-141, fev. 1963.
• MAY, R. M. Simple mathematical models with very complicated dynamics. Nature, v. 261, n. 5560, p. 459-467, jun. 1976.
• LI, T. Y.; YORKE, J. A. Period three implies chaos. American Mathematical Monthly, v. 82, n. 10, p. 985-992, dec. 1975.
• WOLFRAM MATHWORLD. Chaos Theory. Disponível em: https://mathworld.wolfram.com/ChaosTheory.html. Acesso em: 21 maio 2023.
• SCHOLARPEDIA. Chaos Theory. Disponível em: http://www.scholarpedia.org/article/Chaos_theory. Acesso em: 21 maio 2023.
• BAU, David. Chaos and Fractals: An Elementary Introduction. Disponível em: http://www.davidbau.com/complexity/. Acesso em: 21 maio 2023.