Nesse artigo vamos falar sobre ondas, em especial sobre o que é o tipo de onda e sua relação com a EDP das ondas. Em particular, vamos atacar esse assunto de uma forma matemática através da chamada equação da onda. Ademais, nós vamos construir um pouco da teoria das ondas comumente associada a ondulatória física.
O que é o tipo de onda?
Quando falamos de ondas em física ou em matemática entramos num universo rico e com muita discussão próspero para a pesquisa científica. De fato, as ondas configuram-se como importantes modelos físicos para a descrição de fenômenos naturais que perpassam desde a natural aplicação em modelagem ondulatória até fenômenos biológicos como as epidemias.
Nesse sentido, antes de tudo, é necessário que entendermos o que é uma onda. Fisicamente, podemos conceituar uma onda como uma perturbação periódica no espaço-tempo que não transporta matéria.
Todavia, essa definição é suficientemente abrangente, logo, ela contempla diversos tipos de ondas a citar as
- Ondas eletromagnéticas
- Ondas mecânicas
O primeiro tipo de Onda é originalizada a partir de uma perturbação do campo eletromagnético e não necessita de um meio para propagar-se. Por outro lado, as ondas mecânicas são originadas a partir de perturbações na própria matéria, em especial, da sua estrutura atômica.
Nesse mesmo contexto, a concepção de tipo de onda emerge. Uma vez que, a conceituação teórica de uma onda torna-se abrangente. Entretanto, podemos tornar o processo de entendermos esse assunto de uma forma diferente. Em verdade, aqui vamos nos afastar um pouco sobre física e iremos atacar o problema de forma matemática através de uma famosa EDP.
A equação da onda
Agora, vamos começar a entender um pouco melhor as ondas. Para tanto, iremos começar o problema apresentando a EDP da onda, com efeito essa é a seguinte equação
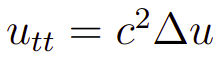
onde u é a solução da EDP da onda (Expressão 1) e o delta representa o operador Laplaciano. Com isso em mãos, podemos entender que uma onda é essencialmente todo objeto matemático u que satisfaz a EDP da Expressão 1.
Em particular, em uma dimensão essa EDP pode ser escrita da seguinte forma

Essa é a EDP da onda em uma única dimensão espacial.
Como resolver a EDP da onda
Agora, tendo em mãos o conhecimento sobre a EDP da onda, podemos começar a nos questionarmos como é possível obter ondas a partir da Expressão 1 ou da Expressão 2. Para fins de simplificação, vamos nos ater a expressão 2 nesse artigo.
Nesse contexto vamos buscar uma forma para obtermos as soluções da expressão 2. Para tanto, iremos empregar o método chamado de separação de variáveis. Esse método se baseia em supor uma forma, relativamente geral, para a solução da EDP da Expressão 2 que é a seguinte

Expressão 3. Forma da solução com separação de variáveis.
Com efeito, essa solução nos leva ao seguinte desenvolvimento pela Expressão 2, vamos considerar c=1 para simplificarmos o procedimento.

Resolvendo as EDOs auxiliares
Agora, veja que a expressão 4 nos dá a seguinte ideia: de um lado temos apenas a derivada de uma função em x e do outro apenas a derivada de uma função em t, nesse sentido, ambas as expressões devem ser constantes, pois, caso contrário deveria-se ter um termo de x no lado direito e um termo com t no lado esquerdo da expressão. Então, podemos fazer a seguinte separação de variáveis:

onde p é uma constante, então reorganizando teremos que

Ou seja, nosso problema se reduz, de uma EDP a resolvermos duas EDOs que essencialmente são da mesma forma, diferindo apenas por conta da da variável dependente. Assim, obter a solução final se reduz a resolvermos a expressão 5 que é feita seguindo o método de solução para uma EDO de segunda ordem de coeficientes constantes, para uma uma função y qualquer

Logo, a solução final de y é a seguinte

Solução “final” para a EDP da onda
Assim, usando esse resultado para as funções fi e g teremos

Agora, veja que com isso temos a seguinte forma para a solução da EDP da onda:

No entanto, os termos A,B, C, D e p são constantes que são especificadas através de condições de contorno e/ou condições iniciais. Em verdade, a partir dessas constantes podemos entender, de fato, como os tipos de ondas surgem.
O tipo de onda como solução da EDP da onda
De fato, a solução por nós obtida na Expressão 7 é uma solução que ainda não contém todos os aspectos físicos que tornam uma onda específica. Assim, é necessário a introdução das condições de contorno e/ou iniciais para que as constantes acima sejam especificadas.
Em geral, essas condições carregam noções físicas importantes como:
- Posição inicial onde a onda estava quando começou a propagar-se,
- Periodicidade da onda,
- Contornos da onda (delimitações espaciais).
Logo, quando introduzimos esses aspectos e especificamos as constantes A,B,C,D e p podemos enfim obter uma solução un para a EDP da onda. Todavia, a equação u é linear, logo pelo princípio de linearidade conseguimos construir uma solução geral para a EDP da onda da seguinte forma:

Consequentemente, essa é a forma típica de uma série de Fourier. Onde a função u que satisfaz a EDP da onda é decomposta numa série de funções periódicas onde cada un é associada a senos e cossenos como mostrado anteriormente.
Com isso, chegamos ao fim gurunauta. Agora, fique sempre ligado na MeuGuru que estamos sempre prontos para te ajudar com a vida universitária.





