Nesse artigo, vamos falar sobre o método da variação dos parâmetros aplicado em EDOs de segunda ordem. De fato, nós já falamos um pouco sobre EDOs não homogêneas, todavia, nos ativemos a falar apenas do método dos coeficientes a determinar. Agora, vamos explorar um método bem mais geral que permitirá a nós obtermos as soluções particulares para uma quantidade muito maior de EDOs de segunda ordem não homogêneas.
Além disso, é sempre bom lembrar que o método da variação é um assunto recorrente em provas de EDOs. Então gurunauta, cola comigo que hoje a MeuGuru preparou esse texto para que você saia daqui manjando muito bem esse assunto e arrasando nas suas provas.
O método da variação dos parâmetros
Em geral, o método da variação dos parâmetros consiste em buscar uma solução particular para uma EDO do tipo
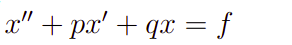
onde x, p, q e f são funções da variável independente t. Basicamente, a solução particular terá a seguinte forma

onde as funções psi são duas soluções Linearmente independentes da EDO homogênea associada. Com isso, nós podemos entender a origem do nome do método. De fato, quando incluímos as funções alfas na Expresão 1 estamos criando uma variação nas soluções da EDO homogênea, uma vez que, as funções alfas agem como parâmetros de variação na nova solução.
Então, o problema desse método consiste em
- Conhecer duas soluções da EDO homogênea.
- Determinar os parâmetros (funções) alfas.
Equações auxiliares para serem resolvidas
Tendo isso em vista, vamos agora obter as expressões gerais para os parâmetros alfas. Para tanto, vamos derivar a forma geral da solução, com efeito.
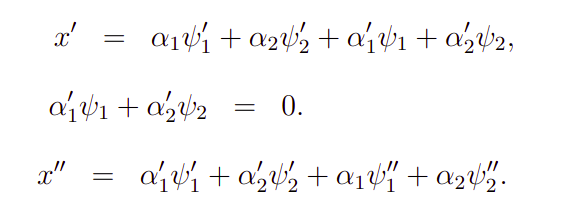
Onde, a condição do meio na Expressão 2 é necessária, uma vez que, ela elimina os termos de alta ordem na segunda derivada. Ademais, levando essas derivadas na EDO geral teremos o seguinte

Ou seja,

e, então, com isso podemos obter o seguinte sistema de equações

Note que, a Expressão 5 é um sistema linear em termos de alfa1′ e alfa2′. Portanto, pode ser facilmente resolvido com os métodos usuais de sistemas lineares. De fato, sua solução são seguintes expressões
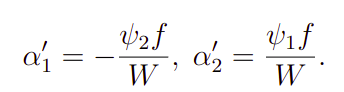
onde W é o wronskiano das soluções psi1 e psi2. Com isso, o problema agora se torna resolver duas equações diferenciais de primeira ordem separáveis.
É importante você ter em mente como prosseguir no método fazendo todo o passo a passo grunauta. De fato, muitos professores exigem isso em suas provas. Por outro lado, caso isso não seja exigido você pode se valer diretamente da expressão 6 e ser feliz com sua solução.
Um exemplo resolvido com variação dos parâmetros
Agora que já vimos o método da variação dos parâmetros, vamos ver um exemplo resolvido passo a passo. Com efeito, consideremos a seguinte EDO com suas duas soluções L.I

veja que essa EDO é não homogênea. Então, precisamos determinar uma solução particular para a parte não homogênea. Para tanto, vamos usar o método da variação dos parâmetros, com a Expressão 6 teremos o seguinte

Assim, a solução particular fica determinada da seguinte forma






