As provas de cálculo, exigem frequentemente os conhecimentos em derivadas derivada e suas aplicações. Assim, o entendimento sobre esse assunto são chaves para você mandar bem naquela prova de cálculo. Então, nesse artigo, vamos falar de duas aplicações da derivada para que você, aprenda de vez o assunto e garanta a aprovação do semestre.
Derivada: Entendendo sua importância e aplicações
A noção matemática da derivada remonta ao surgimento do cálculo com o Físico Isaac Newton. A ideia por trás, consiste em entender como uma função f(x), varia, isto é, muda a medida que os valores de x também mudam. Por mais inocente que essa ideia pareça inocente, ela foi revolucionária, mudou paradigmas e estabeleceu os primeiros passos para várias aplicações em outras áreas como:
- O cálculo integral,
- A mecânica newtoniana,
- Equações diferenciais.
Em especial, tantas aplicações são possíveis, primordialmente, pela versatilidade matemática da derivada. Pois, ela admite diversos sentidos e interpretações, as quais vem tanto da geometria quanto da álgebra.
Assim, já podemos até justificar a necessidade de aprendermos sobre as derivadas no curso de Cálculo. Então, com isso em mente, no resto do artigo vamos ver duas importantes aplicações, para que você possa, enfim, garantir a aprovação em cálculo.
Arrasando na prova: Derivada como inclinação da reta tangente
A primeira aplicação que veremos é associada a geometria das derivadas. Em verdade, a derivada pode ser vista, geometricamente, como o coeficiente angular, ou seja, o declive da reta que tangencia um certo ponto numa curva y=f(x), veja a Figura 1.
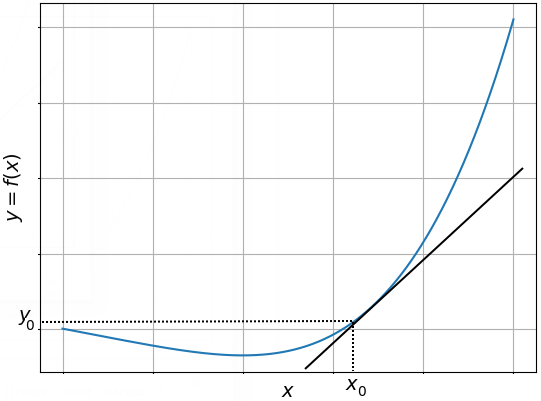
Decerto, essa é uma aplicação importante para o cálculo. Além de ser muito cobrada em provas e exames dessa matéria. Logo, é importante você ter em mente que o obter a equação da reta y=y(x) que tangencia a função no ponto (x_0,f(x_0)) é feito com a seguinte fórmula:
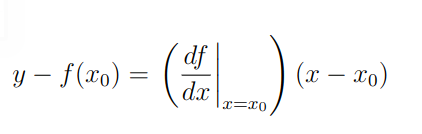
Uma aplicação importante para sua prova: A taxa de variação
Além do sentido geométrico. A derivada também descreve como funções variam, ou seja, como elas se comportam. Isso pode ser visto desde já através da sua definição abaixo.
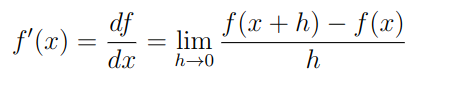
Além disso, é usualmente empregado a notação com uso dos chamados diferenciais, os “d” que acompanham a função. Decerto, eles significam as pequenas variações que a função está sofrendo.
Ademais, a noção da derivada como uma taxa de variação também é importante pois através dela, várias provas podem abordar regras específicas de derivação, em particular, a regra da cadeia. Por exemplo, no caso em que queira-se descobrir como uma função f(r) varia ao longo do tempo t, no entanto, a variável t fica dada em r, ou seja, o que temos é uma função do tipo f(r(t)). Disso, a variação desejada será a seguinte

Agora, que tal ver como uma questão que trata a derivada de uma função como taxa de variação para uma aplicação é resolvida? para isso basta clicar aqui.
Dica de ouro para ir bem nas provas
Então gurunauta, agora que você já está por dentro das aplicações da derivada que tal melhorar a forma de estudar? comece, hoje mesmo, empregando a metodologia Feynman aprenda sobre ela, em apenas 4 passos nesse artigo.





