Fala gurunauta, nesse texto vamos falar das equações diferenciais ordinárias (EDOs). Vamos entender o que são essas equações e conhecer aplicações relevantes nas ciências e engenharias.
O que são equações diferenciais ordinárias?
As equações diferenciais ordinárias, ou simplesmente EDOs, são um tipo específico de equações. De fato, desde o ensino médio nós somos apresentados a várias equações, em particular as equações do segundo grau. Nelas, o grande objetivo que tínhamos era de determinar o famoso valor de x. Analogamente, nas EDOs buscaremos determinar uma incógnita, no entanto, essa incógnita será uma função que estará associada a uma derivada total.
Nesse sentido, uma EDO, para uma função f(t) pode ter a seguinte forma, por exemplo
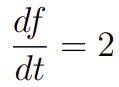
Aqui, talvez seja o momento que você se questione. De fato, a equação acima é algo simples e inclusive, vista em disciplinas como cálculo 1 ou cálculo 2. Em verdade, grande parte das expressões que víamos nessas disciplinas são equações diferenciais ordinárias. Para esse caso sabemos até resolver o problema, basta integrar de ambos os lados e teremos que f(t) = 2t+c, onde c é uma constante.
Entretanto, esse é um caso particular e muito específico das EDOs. Mas, esse já serve como motivação para você entender o espírito do assunto. Pois, inclusive uma EDO pode conter tantas derivadas quanto queiramos. Assim, podemos definir uma equação diferencial ordinária como sendo uma equação do seguinte tipo:
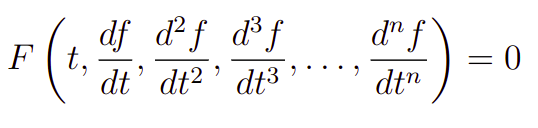
onde F é uma regra geral que associa todos os n+1 argumentos do parênteses. A função f, que é associada as derivadas é chamada de solução da equação diferencial e, em muitos casos, é ela que queremos obter. A variável t é chamada de variável independente e a solução f é dita ser a variável dependente.
Um ponto chave sobre essas equações é que elas podem ser classificadas de acordo com suas características. Tendo isso em vista, vamos ver alguns tipos e classificações de EDOs.
Tipos e classificação de EDOs
Uma equação diferencial ordinária pode ser de dois tipos: Linear ou não Linear. Dizemos que uma EDO é linear se ela tem a seguinte forma

Isto é, cada termo que multiplica as derivadas é uma função da variável independente t. Caso, ocorra que algum dessas funções p seja do tipo p=(f,t) dizemos que a EDO é não linear.
Ademais, podemos ainda classificá-la quanto a sua ordem. A ordem de uma EDO é o número da ordem da derivada mais alta existente. Com efeito, no caso da Figura 2 a derivada tem ordem n e da Figura 1 a ordem é 1.
Além disso, as EDOs podem ser classificadas ainda quanto a sua homogeneidade. Em particular, a EDO da Figura 2 é dita não homogênea pois apresenta um termo, q(t), que contém apenas a variável independente e não está associado a função f (variável dependente). A versão homogênea da EDO da Figura 2 é a seguinte:
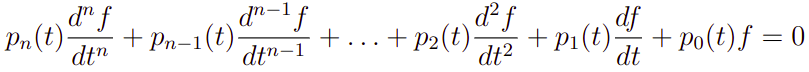
Por fim, também temos o chamado grau de uma EDO. O grau corresponde ao número em que o termo da derivada está elevando, por exemplo:
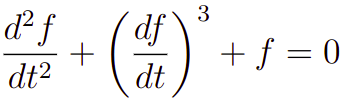
o grau é 3, pois, é o valor o expoente mais alto que algum termo de f está elevado.
Os principais problemas da teoria das equações diferenciais ordinárias
A teoria das equações diferenciais ordinárias é muito importante e significativa. De fato, aqui há poucas linhas para falarmos sobre o assunto com sua totalidade. Entretanto, para esse primeiro texto, que constituirá uma série de artigos sobre as elegantes e belíssimas EDOs, vamos nos ater a explicitar os principais problemas dessa teoria.
Na verdade, aqui estamos nos referindo as principais questões que queremos responder para caso tenhamos uma EDO. Com efeito, esses são:
- Dada uma equação diferencial ordinária qualquer, existe uma solução para ela?
- Dado uma equação diferencial ordinária que tenha solução, essa solução é única?
- Como é possível resolver uma equação diferencial ordinária qualquer?
Esses pontos podem parecer estranhos a primeira vista. De fato, se perguntar se existe solução? como é possível resolver? e se a solução é única? . Bom amigos, na matemática nem tudo são flores. Em verdade, não são todas as equações diferenciais que terão solução, além de que sequer há um método geral para resolver qualquer EDO. Tá vendo por que eu disse que eu tinha poucas linhas?, no entanto, os esforços incansáveis de matemáticos e físicos trouxeram luz a essas respostas e com isso hoje conhecemos alguns métodos de solução e também conseguimos determinar se uma EDO terá solução única ou não.
Mas desde já, tenha em mente uma coisa. As equações que nós conseguimos resolver, de forma analítica, isto é, com papel e caneta, é suficientemente pequena. Por isso, há teorias como a teoria qualitativa que descobrem o comportamento das soluções sem sequer resolver a EDO. Inteligente não é?, de fato, esse mundo é fascinante.
Aplicações das equações diferenciais ordinárias
As equações diferenciais ordinárias são extremamente significativas para vários contextos das ciências. Em suma, elas surgiram com um propósito aplicado de descrever movimentos de corpos. Todavia, seu poder matemático, principalmente com o surgimento da modelagem, tornou elas incrivelmente versáteis e tendo ramificações para várias áreas. Vamos destacar agora, algumas aplicações dessas:
- Dinâmica de osciladores harmônicos e circuitos elétricos;
- Dinâmica populacional de indivíduos, competição entre espécies, vírus e doenças;
- Movimento de corpos na mecânica clássica;
- Modelagem de tremores e abalos sísmicos em prédios;
- Resfriamento e aquecimento de corpos;
- Decaimento radioativo;
- Curvas, envoltórias e trajetórias ortogonais;
- Sistemas mecânicos e elétricos de engenharia como o oscilador de Duffing.
Então gurunauta, espero que você tenha gostado desse texto e lembre-se de sempre contar com a MeuGuru para te dar aquela força no fim do semestre.





