Nesse artigo, vamos falar sobre o Teste da razão para séries numéricas. De fato, dentro do assunto de séries numéricas o teste da razão desempenha um papel protagonista na solução de diversos problemas de convergência de séries. Tendo isso em vista, é muito importate que você gurunauta, saiba aplicar esse teste com maestria e assim garanta o tão sonhado 10 em sua prova.
Portanto, vamos vem comigo que vou te ajudar nesse assunto.
Entendendo o que são as séries numéricas (Revisão básica)
Primeiramente, vamos entender o que de fato são séries numéricas. Com efeito, a ideia aqui é pensarmos num tipo especial de sequência numérica. Então, vamos considerar uma sequência (xn) daí, vamos construir uma segunda sequência (Sn) cujos termos são dados a seguir
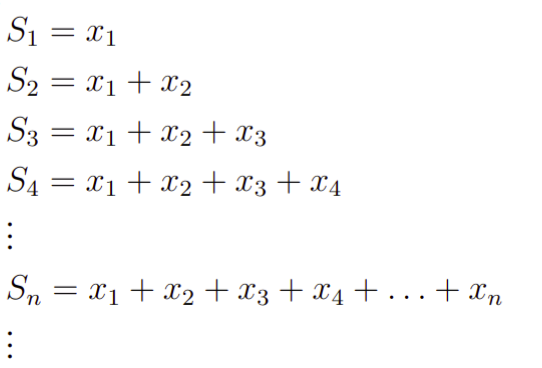
isto é, cada termo de (Sn) é a soma dos elementos da sequência (xn) até o elemento n-ésimo. A sequência (Sn) assim construída é chamada de sequência das reduzidas. Além disso, a partir de (Sn) vamos construir a noção de série numérica, para tanto, vamos fazer o limite de n para o infinito, com efeito

Nesse sentido, podemos definir as séries numéricas como uma soma infinita de termos obtido a partir de uma sequência numérica (xn). Todavia, assim como estudamos sequências em séries numéricas também temos um problema fundamental: determinar quando uma série é convergente.
As séries numéricas convergentes
Em verdade, na maioria das questões desse assunto, seu trabalho será determinar se uma série específica é ou não convergente. Isto é, se o a soma da expressão 2 é um valor S finito. Mas, veja fazer isso nem sempre é uma tarefa fácil, nesse sentido há uma gama de resultados que podem ser empregados com a finalidade de garantir que esses resultados de convergência sejam estabelecidos, em particular citamos os seguintes Testes
- Razão,
- Integral,
- Raíz,
- Critério das séries alternadas de Leibniz,
- Critério da comparação,
- Comparação no limite,
- Critério da divergência (assegura uma condição necessária, mas não suficiente)
- Critério das somas telescópicas,
- Teste das p-séries
Como você pode ver, essa teoria comporta diversos testes. Nesse sentido, vamos nos ater ao primeiro teste o qual pode ser usado em uma gama de séries e assim sendo uma ótima carta na manga para esses problemas.
Teste da razão para séries
O teste da razão serve, basicamente para qualquer série numérica. Nesse sentido, vamos enunciá-lo a seguir em forma de um elegantíssimo Teorema.

Note que esse teste sugere um cálculo de um limite. Tendo isso em vista, você sempre deverá calcular esse limite e entender em que caso o valor L obtido se encaixa.
Exemplos resolvidos com o teste da razão para séries numéricas
Com a finalidade de entendermos esse Teorema, vamos fazer alguns exemplo resolvidos. Primeiramente, vamos ver os casos (i) e (ii) do Teorema anterior.
Então, vamos avaliar a convergência da série

para isso, vamos usar o teste da razão, com efeito temos

Logo, segue do item (i) que a série avaliada é convergente. Agora, vamos ver o caso da série

novamente, usando o teste da razão teremos

Patologias importantes para o teste da razão
O critério (iii) do teste dá um caráter inconclusivo. De fato, caso você ache em seus cálculos que o limite L seja igual a 1 você não poderá intuir nada sobre a convergência ou divergência a série. Em suma, esse resultado é apenas um indicativo de que você deve usar outro teste.
Para exemplificarmo isso, vamos avaliar a série harmônica, que sabemos ser divergente, com o teste da razão. Com efeito,

Logo, pelo critério (iii) não podemos intuir nada sobre a convergência dessa série.
Ademais, podemos ver ainda um outro caso interessante que é uma variação da série harmônica onde o termo geral tem a forma (-1)n1/n. De fato, essa série é convergente e sua convergência pode ser feita com uso do teste de Leibniz para séries alternadas. Todavia, se aplicamos o teste da razão nós temos

visto que |-1| = 1. Portanto, novamente temos o caráter inconclusivo do teste sendo evidenciado.
Então gurunauta, nada de dizer que uma série converge ou diverge se você obter L=1 viu?, caso isso aconteça procure outro teste para avaliar.
E lembre-se gurunauta, sempre conte com a MeuGuru para te ajudar com os problemas da vida universitária. Agora, você não está mais sozinho sempre terá um Guru especial para te ajudar!.





