Resistência dos materiais, como disciplina, é essencial para calcular tensões e deformações em estruturas e componentes mecânicos. Assim, na estática, o conceito de equilíbrio estático foi definido e a diferença entre forças internas e externas foi introduzida. No entanto, é crucial entender que não é suficiente calcular apenas as forças para avaliar a integridade estrutural de um componente ou estrutura.
Isso porque, os desintendidos, geralmente se refere apenas a se o componente (viga, ponte, colunas, dentre outras estruturas) pode suportar as cargas aplicadas ou se deformará além do limite permitido, ou até mesmo se quebrará. Dessa maneira, a resistência dos materiais, portanto, se destaca como um tema central para estudos mecânicos e engenharia mecatrônica, pois nos permite determinar, por meio de cálculos, se os componentes projetados funcionarão conforme planejado ou falharão.
Assim, para isso, é essencial definir o termo estresse como uma medida de força interna por área atuando dentro de uma estrutura. Então, convertendo essas forças internas em tensões por meio de cálculos, obtemos uma medida que, ao contrário das forças, pode estar relacionada às características materiais, que podemos medir ou consultar.
Além disso, devemos considerar o problema relacionado ao cálculo de deformações em componentes e estruturas. Dessa maneira com base nas deformações calculadas, importante entender como calcular as deformações como uma medida de quão significativas. Em relação às dimensões do componente considerado.
O conceito de equilíbrio estático no contexto resistência dos materiais
Primeiramente, pela estática, compreendemos que as três relações a seguir se aplicam quando um sistema mecânico plano está em equilíbrio estático.
[latexpage]
\[
\sum f_{x} = 0
\]
\[
\sum f_{y} = 0 ;
\]
\[
\sum M_{z} = 0
\]
Basicamente, isso implica que podemos resumir todas as forças na direção de um plano cuidadosamente escolhido no sistema de coordenadas e, além disso, calcular a soma dos momentos em torno de um ponto de nossa escolha. Assim, essa abordagem se tornou nossa principal ferramenta para calcular forças e momentos de reação em estruturas sujeitas a cargas externas. Dessa maneira, podemos estender o equilíbrio plano para três dimensões adicionando o equilíbrio de dois momentos e um equilíbrio de força adicional.
[latexpage]
\[
\sum M_{x} = 0
\]
\[
\sum M_{y} = 0 ;
\]
\[
\sum f_{z} = 0
\]
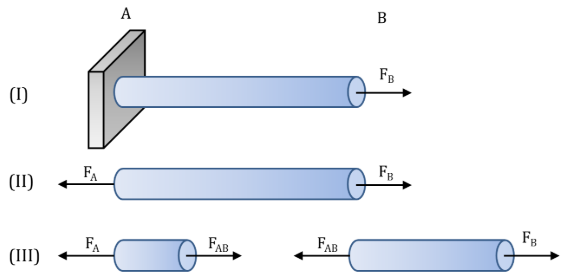
Assim, é importante observar como o conceito de equilíbrio estático também serve como base para o cálculo de forças internas. Se considerarmos uma barra submetida a uma única carga axial, conforme mostrado na Figura, as equações anteriores (de equilíbrio) nos permite calcular a força de reação em A. Assim, fazemos isso desenhando um diagrama de corpo livre, e escrevendo uma única equação de equilíbrio com uma única incógnita: a força de reação FA.
No entanto, agora vamos imaginar que introduzimos um corte imaginário entre os pontos A e B, dividindo a barra em duas partes, conforme mostrado na Figura 1-1-III. Dessa maneira, ambas as seções devem permanecer em equilíbrio estático, o que só pode ser mantido se uma força atuar no corte que aplicamos. Essas forças atuam dentro do material e, portanto, são chamadas de forças internas, contrárias às cargas aplicadas, que são chamadas de forças externas. Por fim, essas são as forças que usaremos para os cálculos de estresse. Entretanto, antes de proseguir precisamos definir o que é “estresse”.
Resistência dos Materiais : A definição de estresse de Cauchy
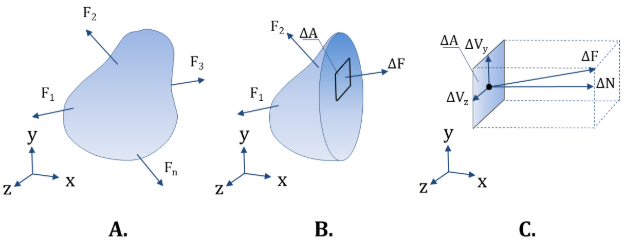
Primeiramente, consideraremos um corpo elástico sujeito a forças externas F1… Fn. Tradicionalmente, é normal representar esse corpo em um forma aleatória (no nosso caso parece uma batata?), mas pode assumir qualquer formato (Figura 2-A). Assim, se adicionarmos um corte (imaginário) através do corpo (Figura 2-B), forças internas devem atuar na seção para manter o equilíbrio. Então, por uma questão de simplicidade, agora definiremos um sistema de coordenadas com o eixo x normal à seção e os eixos y e z no plano da seção (Figura 2-C).
Vamos agora considerar ΔF como a força interna na área ΔA que atua dentro do material. Podemos definir uma tensão normal à seção. Isso é, em média, dado por:
[latexpage]
\[
\sigma _{av} = \frac{\Delta N}{\Delta A}
\]
Chamamos este componente de tensão normal (afinal, são forças normais atuando). Assim, as duas forças internas agindo paralelamente à seção são chamadas de forças cortantes. As tensões de cisalhamento correspondentes, em média, são dadas por:
[latexpage]
\[
\tau _{y,av} = \frac{\Delta V_{y}}{\Delta A }
\]
\[
\tau _{z,av} = \frac{\Delta V_{z}}{\Delta A }
\]
Para um ponto P dentro da área ΔA, os componentes de tensão podem agora ser definidos como valores de ponto ao deixar o tamanho da área chegar a zero. Cauchy definiu as tensões da seguinte maneira:
[latexpage]
\[
\sigma _{x} = \displaystyle \lim_{\Delta A \to 0} \frac{\Delta N}{\Delta A}
\]
\[
\tau _{y} = \displaystyle \lim_{\Delta A \to 0} \frac{\Delta V_{y}}{\Delta A}
\]
\[
\tau _{z} = \displaystyle \lim_{\Delta A \to 0} \frac{\Delta V_{z}}{\Delta A}
\]
Dessa maneira, é possível observar que:
- O cálculo da tensão é baseado em forças internas.
- As tensões são divididas em componentes normais e de cisalhamento.
Forças internas definidas em termos de tensões
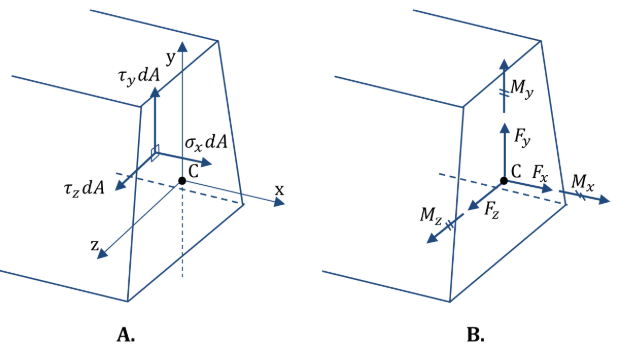
Agora, depois de termos tido uma ideia do que é um estresse, notamos que o estresse frequentemente, na verdade, normalmente, irá variar ao longo da seção considerada. Assim, se as tensões forem conhecidas, também podemos definir as forças internas como três componentes de força e três componentes de momento em termos de tensões.
No entanto, dado que estas variam, teremos que considerar todos os segmentos de área infinitesimalmente pequenos na seção e somar todos os termos de área de força multiplicados. Dessa maneira, isso parece tão tedioso quanto é, e felizmente podemos usar a integração para resolver esta tarefa e integrar uma distribuição de tensão conhecida ao longo de uma seção transversal para obter forças e momentos.
Com base na Figura 3, isso nos dá as seguintes relações:
[latexpage]
\[
F_{x} = \int \sigma _{x} dA
\]
\[
F_{y} = \int \tau _{xy} dA
\]
\[
F_{z} = \int \tau _{xz} dA
\]
\[
M_{x} = \int (y \tau _{xz} – z \tau _{xy})dA
\]
\[
M_{y} = \int z \sigma _{x}dA
\]
\[
M_{z} = \int ( -yz \sigma _{y}) dA
\]
Isso pode parecer um pouco abstrato por enquanto, mas mais tarde, essa definição é exatamente o que é necessário para derivar as fórmulas básicas de projeto para cálculos de tensão em pilares e vigas.
Tensões principais
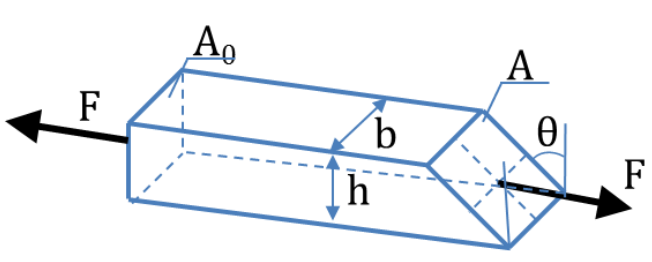
Primeiramente, consideraremos uma barra carregada axialmente contendo uma seção oblíqua, como mostrado na Figura 4. Assim, as tensões normais e de cisalhamento na seção oblíqua, obtidas determinando a projeção da força F nas direções normais e paralelas à seção.
Dessa maneira, essas projeções divididas pela área da seção oblíqua para obter as tensões normais e de cisalhamento. Obtemos as duas expressões a seguir:
[latexpage]
\[
\sigma = \frac{F cos\theta }{\frac{A_{0}}{cos\theta }} = \frac{F}{A_{0}}cos^{2}\theta
\]
\[
\tau = \frac{F sen\theta }{A} = \frac{F sen\theta }{\frac{A_{0}}{cos\theta}} = \frac{F}{A_{0}}cos\theta sen\theta
\]
As tensões observadas como funções harmônicas do ângulo da seção θ. Se traçarmos as tensões para valores variados de θ, obtemos resultados conforme mostrado na Figura 1-5. Por fim, observamos o seguinte:
- As tensões dependem da orientação da seção.
- Uma direção para a qual as tensões de cisalhamento desaparecem e nos deixam com um estado de pura normalidade é chamada de direção principal. As tensões normais correspondentes são chamadas de tensões principais.
Assim, nesse sentido, a primeira direção principal é a direção axial na qual a carga é aplicada, e a tensão principal correspondente é F/A0. Então, a segunda direção principal é perpendicular à primeira direção, e a tensão principal correspondente é 0. Dessa forma, observa-se que a tensão de cisalhamento é zero em ambas as direções principais. Então, uma transformação para coordenadas principais nos fornece tensões normais máximas e nenhum cisalhamento.
Princípio de Saint-Venant e a resistência dos materiais
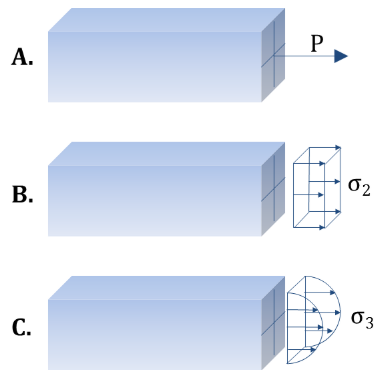
Este princípio, em um sentido qualitativo, trata da correspondência entre as tensões e os meios pelos quais as cargas são aplicadas a uma determinada estrutura. Dessa maneira, o princípio de Saint Venant afirma que uma carga aplicada em diferentes formas causará variação local nas tensões apenas nas proximidades da área de aplicação.
A uma distância do ponto ou área de ação, as tensões permanecerão, no entanto, as mesmas, não importa o método pelo qual a carga foi aplicada.
Assim, poderíamos também dizer que a parte restante da estrutura “não se importa” com a forma como a carga é adicionada. Dessa maneira, para a barra da Figura 5, as tensões em uma seção transversal a uma distância da área onde a carga, aplicada iguais se a seguinte condição for atendida:
[latexpage]
\[
P = \int \sigma _{2} dA = \int \sigma _{3} dA
\]
Por fim, isso acaba sendo extremamente útil em muitos contextos. Então, o princípio de Saint-Venant permite-nos substituir uma força que atua sobre uma pequena parte de uma estrutura por uma carga equivalente, facilitando o manuseio em nossos cálculos, sem afetar as tensões em nível global. Dessa maneira, vamos a alguns exemplos de falhas e planejamentos.
Exemplos históricos da resistência dos materiais
Falha dos navios Liberty
Primeiramente, os aços dúcteis podem tornar-se quebradiços devido a baixas temperaturas ou tratamento térmico inadequado. Dessa maneira, os navios Liberty, exemplos de falhas frágeis em chapas metálicas soldadas durante a Segunda Guerra Mundial, à medida que o processo de soldagem estava sendo desenvolvido. Entretanto, comportamento do material frágil é detectado por testes de impacto (denotado resistência à fratura). Durante as investigações de falha, descobriu-se que a chapa metálica no estado pós-soldagem deveria obter uma resistência à fratura de 27 Joule em um teste de impacto Charpy-V para ser adequada ao propósito.
Falha por fadiga da plataforma de perfuração Alexander-Kielland
A plataforma de perfuração semissubmersível Alexander Kielland virou em 1980 enquanto estava em operação no Campo Ekofisk na plataforma continental norueguesa, matando mais de 100 pessoas. Nesse ínterim, a comissão de investigação concluiu que uma órtese (mostrada abaixo) havia fraturado perto de uma posição onde os eletricistas montaram um hidrofone (equipamento de medição) soldando próximo a um bueiro. A soldagem mal conduzida, em combinação com a concentração de tensão do poço de visita, reduziu ao máximo o tempo de vida em fadiga do contraventamento, onde a falha ocorreu enquanto a plataforma estava em serviço (embora o fator de segurança contra fadiga para estruturas offshore no Mar do Norte geralmente seja 10).
Referências sobre a resistência dos materiais:
- https://www.nuclear-power.com/nuclear-engineering/materials-science/material-properties/strength/
- https://efficientengineer.com/strength-of-materials/
- https://www.hochschule-rhein-waal.de/introduction_to_strength_of_materials.pdf
- https://vardhaman.org/wp-content/STRENGTH-OF-MATERIALS-1.pdf
- https://www.sciencedirect.com/topics/materials-science/mechanical-strength
- https://mathalino.com/mechanics-and-strength-of-materials/mechanics-and-strength-of-materials#google_vignette
- https://mechanicalc.com/reference/strength-of-materials
