Cordas vibrantes são um dos tópicos principais dentre os assuntos de física 2. Certamente, dentro da física 2 há diversos assuntos relevantes que permeiam a hidroestática, acústica, termometria, termodinâmica e ondulatória. Em particular, esse último assunto é essencialmente rico em aplicações e subtópicos que permiam uma vasta quantidade de assuntos dentro da física ondulatória.
Então, tendo isso em vista, nós da MeuGuru decidimos elaborar esse texto especialmente para você gurunauta que está vendo Física 2 agora ou logo logo estará encarando essa disciplina. Nesse sentido, decidimos trazer nesse texto um tutorial rápido sobre um tópico muito relevante da Física 2: ondas em cordas, ou também as cordas vibrantes. Ou seja, pode se preparar que hoje vamos entrar fundo na física ondulatória percorrendo os conceitos fundamentais das cordas vibrantes e, ainda, veremos na prática alguns exercícios resolvidos.
Por que estudar cordas vibrantes ?
Dentro do escopo da ondulatória é essencialmente significativo que consigamos estudar ondas sejam essas eletromagnéticas (ondas que não necessitam de meio para se propagar e são oriundas das oscilações dos campos elétricos e magnéticos) ou mecânicas (tipos de oscilações que necessitam de um meio material para propagar-se).
Decerto, não é possível, por vezes, que consigamos fácil acesso a qualquer tipo de onda para podermos estudá-la. Entretanto, há alguns casos particulares e simples que permitem que nós consigamos estudar propriedades das ondas em sistemas físicos simples que, podem ser reproduzidos com uso de poucos recursos. Nesse sentido, as cordas vibrantes emergem como um problema simples capaz de capturar a física de diversos sistemas como ondas eletromagnéticas e permitindo a nós compreendermos os processos envolvidos na propagação de ondas.
Oscilações unidimensionais em uma corda
Então, feita a dicussão inicial vamos agora entender como ocorrem oscilações em uma corda. Com efeito, essas oscilações possuem algumas características que elencamos na lista a seguir:
- Unidimensionais. Uma vez que, consideramos como uma corda um objeto retilíneo e inextensível (cujo comprimento não é modificado) segue que o mesmo configura-se como unidimensional, visto que o comprimento da corda é muito maior que o raio da sua secção transversal.
- O perfil das oscilações em cordas é transversal. Sem dúvida, ao passo que seu comprimento é inextensível a única forma de produzirmos oscilações e, consequentemente, ondas em cordas é através de pulsos aplicados de forma transversal. Nesse sentido, veja a figura a seguir que exemplifica o processo de geração de pulsos de ondas em cordas.
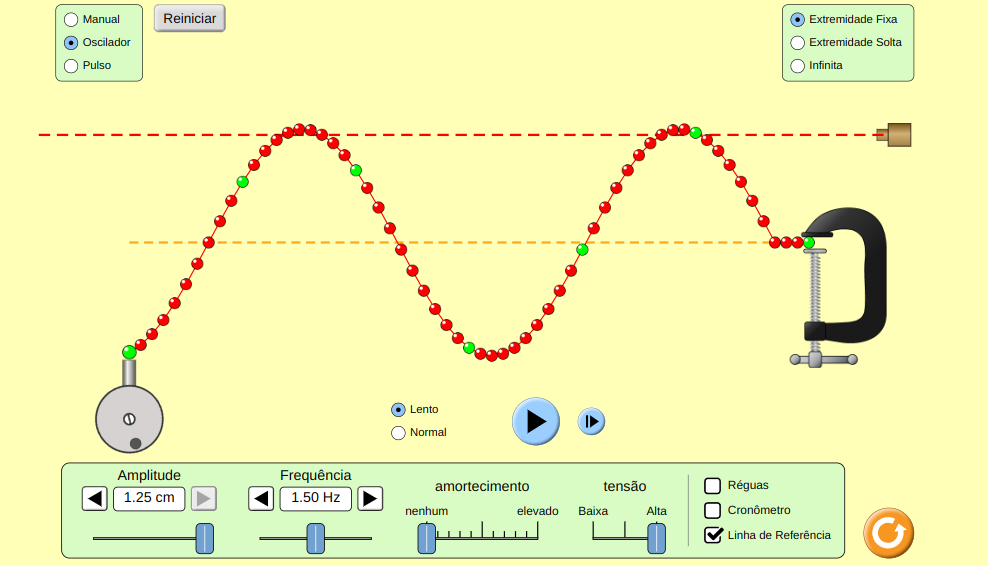
Observe que, em geral estudamos o problema de cordas vibrantes tendo uma extremidade fixa e outra não. Entretanto, é importante ressaltar que há problemas em que ambas as extremidades podem estar fixas como é o caso de ondas estacionárias.
Alguns aspectos matemáticos das ondas em cordas vibrantes
Ondas em cordas tem sua propagação descrita pela equação da onda (EDP da onda) restrita ao caso unidimensional, tornando-se uma EDP de segunda ordem conforme mostramos a seguir.
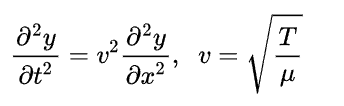
em que μ é a densidade linear da corda e T é a tensão aplicada na corda para geração do pulso e v é a velocidade de propagação da onda na corda. Ademais, a solução para essa equação pode ser determinada com uso de alguns métodos de EDPs como o método de separação de variáveis e séries de Fourier. Em geral, nosso interesse, no contexto de um curso de Física 2, é apenas de conhecer a solução cujo forma geral é a seguinte.
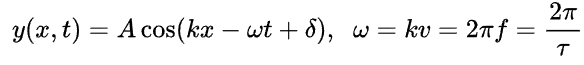
em que ω é a frequência angular de oscilação, k é uma constante associada ao número de onda (2 pi /comprimento de onda), A é o termo que determina a amplitude de oscilação do eixo y e δ é associado a defasagem da posição inicial com relação a posição de equilíbrio da oscilação. Vale ressaltar que, é possível expressarmos essa solução como uma função seno, apenas modificiando as constantes adequando-as conforme a necessidade e fazendo uso de algumas relações trigonométricas.
Exercícios resolvidos sobre cordas vibrantes
Agora, tendo em vista que conheçemos alguns aspectos gerais de cordas vibrantes vamos te mostrar como você pode resolver problemas desse tópico. Com efeito, vamos considerar um problema clássico dentre o estudo de ondulatória e, mais especificamente, da propagação de ondas em cordas, esse problema apresentamos o enunciado a seguir.
[Extraída de (YOUNG, FREEDMAN, 2016) ] Uma corda de 1,50 m e peso 1,25N está amarrada ao teto pela sua extremidade superior, e a inferior sustenta um peso P. Despreze a pequena variação na tensão pelo comprimento da corda, produzida pelo seu peso. Quando a corda é puxada suavemente, as ondas que se deslocam para cima obedecem à equação: y(x, t)=(8,5mm) cos (172rad/m x-4830rad/s t) . Suponha que a tensão da corda seja constante e igual a P.
- (a) Quanto tempo leva para um pulso percorrer toda a extensão da corda?
- (b) Qual é o peso P ?
- (c) Quantos comprimentos de onda há sobre a corda em qualquer instante?
- (d) Qual é a equação para ondas que se deslocam para baixo na corda?
Resolução do problema!
Então, vamos agora resolver esse problema. De fato, é fácil ver que ao termos uma equação da onda dada é possível identificar as seguitnes constantes, com relação a equação de onda completa que viemos anteriormente, sendo essas: A = 8.5mm, k = 172rad/m, ω = 4830 rad/s. De posse disso vamos resolver cada item.
O item (a) é resolvido facilmente resolvido uma vez que identificamos as constantes na equação de onda dada. Então, como a corda tem comprimento L=1.5m vamos determinar o tempo t para que a onda que possui comprimento de onda associado ao número de onda k, assim, o cálculo para essa solução é o seguinte:
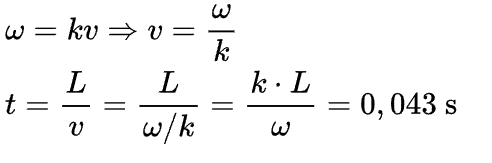
em que substituimos os valores numéricos apenas ao fim da conta.
Prosseguindo, ao item (b) podemos determinar o peso P pedido através da tensão na corda visto que a tensão na corda é exatamente o peso P. Logo, segue da relação da velocidade de propagação de uma onda numa corda que
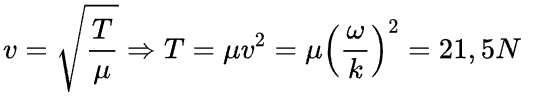
e concluímos o item (b). Agora, para o item (c), podemos determinar a quantidade n de comprimentos de onda fazendo a razão entre o comprimento L da corda pelo comprimento de onda, assim, temos o seguinte cálculo.
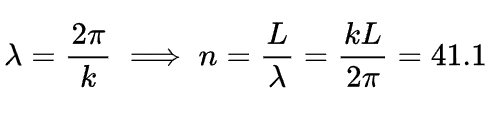
Por fim, vamos então seguir para o último item. Com efeito, esse item é simples para resolvermos pois envolve apenas conhecimentos teóricos e sequer exige cálculos. Para tanto, basta ver que ondas que se propagam para cima são tais que o sinal do termo de frequência angulaar é positivo, logo a equação que buscamos é simplesmente y(x, t)=(8,5mm) cos (172rad/m x+4830rad/s t).
Referências
- NUSSZENZVEIG, Moysés. Curso de Física Básica – Volume 2: Fluidos, Ondas e Calor. 6ª ed. São Paulo: Edgard Blücher, 2013. 400 p.
- FEYNMAN, Richard Philips. Física em 12 lições: fáceis e não tão fáceis. 3. ed. Rio de Janeiro: Nova fronteira, 2021. 293 p. ISBN: 9786556401614.
- YOUNG, Hugh D; FREEDMAN, Roger A. Sears e Zemansky. Física, Volume 2: Termodinâmica e Ondas. 14.ed. São Paulo: Pearson, 2016. 560 p. ISBN: 9788543005683.
- HALLIDAY, David; RESNICK, Robert; WALKER, Jearl. Fundamentos de física. Volume 2. 9. ed. Rio de Janeiro: LTC, 2012.